题目内容
19．
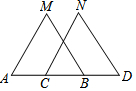如图，在△ABM和△CDN中，A，C，B，D在同一条直线上，MB=ND，MA=NC，则下列条件中能判定△ABM≌△CDN的是（ ）| A． | ∠MAB=∠NCD | B． | ∠MBA=∠NDC | C． | AC=BD | D． | AM∥CN |
分析 根据普通三角形全等的判定定理，有AAS、SSS、ASA、SAS四种．逐条验证．
解答 解：A、MB=ND，MA=NC和∠MAB=∠NCD，不能判定△ABM≌△CDN，故A选项不符合题意；
B、MB=ND，MA=NC和∠MBA=∠NDC，不能判定△ABM≌△CDN，故B选项不符合题意；
C、由AC=BD可得AB=CD，利用SSS能判定△ABM≌△CDN，故C选项符合题意；
D、AM∥CN，得出∠MAB=∠NCD，结合MB=ND，MA=NC不能判定△ABM≌△CDN，故D选项不符合题意．
故选：C．
点评 本题考查了全等三角形的判定；三角形全等的判定是中考的热点，一般以考查三角形全等的方法为主，判定两个三角形全等，先根据已知条件或求证的结论确定三角形，然后再根据三角形全等的判定方法，看缺什么条件，再去证什么条件．
练习册系列答案
相关题目
9．-$\frac{1}{3}$的倒数是（ ）
| A． | 3 | B． | $\frac{1}{3}$ | C． | -3 | D． | -$\frac{1}{3}$ |
10．已知方程x2k-1+k=0是关于x的一元一次方程，则方程的解是（ ）
| A． | -1 | B． | $-\frac{1}{2}$ | C． | $\frac{1}{2}$ | D． | 1 |
7．已知sinA=$\frac{1}{2}$，则∠A的度数为（ ）
| A． | 30° | B． | 45° | C． | 60° | D． | 90° |
14．
若实数a，b在数轴上的位置如图所示，则下列判断正确的是（ ）
若实数a，b在数轴上的位置如图所示，则下列判断正确的是（ ）| A． | a＞0 | B． | ab＞0 | C． | a＜b | D． | a，b互为倒数 |
11．下列四选项中，以三个实数为边长，能构成直角三角形的是（ ）
| A． | $\sqrt{3}$，2，$\sqrt{5}$ | B． | $\sqrt{1}$，$\sqrt{2}$，$\sqrt{3}$ | C． | $\sqrt{6}$，$\sqrt{8}$，$\sqrt{10}$ | D． | 3，4，6 |