题目内容
14.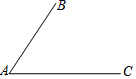 如图,已知线段AB,AC
如图,已知线段AB,AC(1)作⊙O使得线段AB,AC为⊙O的两条弦(要求尺规作图,保留作图痕迹)
(2)在(1)中的⊙O上找出点D,使得点D到A、B两点的距离相等
(3)在(2)中,若AB=8,⊙O的半径为5,求△ABD的面积.
分析 (1)根据弦的垂直平分线经过圆心,先作出两条弦的中垂线,其交点即为圆心;
(2)根据垂直平分线上任意一点,到线段两端点的距离相等,即可得出点D;
(3)根据垂径定理以及勾股定理,即可得出△ABD的AB边长的高,进而得出△ABD的面积.
解答 解:(1)如图所示,⊙O即为所求;
(2)如图所示,点D1,D2即为所求;
(3)如图所示,连接AO,则AO=5,
∵AB⊥D1D2,AB=8,
∴AE=4,
∴Rt△AOE中,OE=3,
∴D1E=5-3=2,D2E=5+3=8,
∴△ABD1的面积=$\frac{1}{2}$×8×2=8,
△ABD2的面积=$\frac{1}{2}$×8×8=32,
故△ABD的面积为8或32.
点评 本题主要考查了复杂作图,线段垂直平分线的性质以及垂径定理的综合应用,解决此类题目的关键是熟悉基本几何图形的性质,结合几何图形的基本性质把复杂作图拆解成基本作图,逐步操作.解题时注意:垂直弦的直径平分这条弦,并且平分弦所对的两条弧.

练习册系列答案
 特高级教师点拨系列答案
特高级教师点拨系列答案
相关题目
5.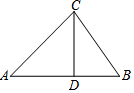 如图,在△ABC中,CD⊥AB于点D,己知AC=a,∠A=α,∠B=β,则BD的长是( )
如图,在△ABC中,CD⊥AB于点D,己知AC=a,∠A=α,∠B=β,则BD的长是( )
 如图,在△ABC中,CD⊥AB于点D,己知AC=a,∠A=α,∠B=β,则BD的长是( )
如图,在△ABC中,CD⊥AB于点D,己知AC=a,∠A=α,∠B=β,则BD的长是( )| A. | $\frac{a•sinα}{tanβ}$ | B. | $\frac{a•cosα}{tanβ}$ | C. | a•sinα•tanβ | D. | a•cosα•tanβ |
2.下列计算正确的是( )
| A. | 6-(-6)=0 | B. | (-2.8)+1.2=1.6 | C. | (+2)+(-5)=-3 | D. | $\frac{1}{3}-({-\frac{2}{3}})=-\frac{1}{3}$ |
 一个长方形的周长是12 cm,一边长是x( cm).
一个长方形的周长是12 cm,一边长是x( cm).