某校图书馆的藏书在两年内从5万册增加到7.2万册.设平均每年藏书增长的百分率为x.则依据题意可得方程5(1+x)2=7.2．题目和参考答案——青夏教育精英家教网—

题目内容

6．某校图书馆的藏书在两年内从5万册增加到7.2万册，设平均每年藏书增长的百分率为x，则依据题意可得方程5（1+x）²=7.2．

分析利用平均增长率问题，一般用增长后的量=增长前的量×（1+增长率），参照本题，如果设平均每年增长的百分率为x，根据“某校图书馆的藏书在两年内从5万册增加到7.2万册”，即可得出方程．

解答解：设平均每年增长的百分率为x；
第一年藏书量为：5（1+x）；
第二年藏书量为：5（1+x）（1+x）=5（1+x）²；
依题意，可列方程：5（1+x）²=7.2．
故答案为：5（1+x）²=7.2．

点评本题考查了由实际问题抽象出一元二次方程中求平均变化率的方法．若设变化前的量为a，变化后的量为b，平均变化率为x，则经过两次变化后的数量关系为a（1±x）²=b．

练习册系列答案

自我评价与提升系列答案

相关题目

方程两根的情况	对应的二次函数的大致图象	a，b，c满足的条件
方程有两个不相等的负实根		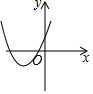$\left\{\begin{array}{l}a＞0\\△={b^2}-4ac＞0\\-\frac{b}{2a}＜0\\ c＞0.\end{array}\right.$
方程有一个负实根，一个正实根		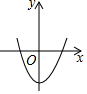$\left\{\begin{array}{l}a＞0\\ c＜0.\end{array}\right.$
方程有两个不相等的正实根		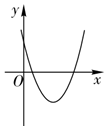$\left\{\begin{array}{l}a＞0\\△={b^2}-4ac＞0\\-\frac{b}{2a}＞0\\ c＞0.\end{array}\right.$