题目内容
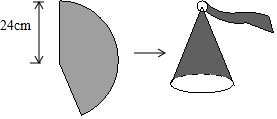
11. 如图,在△ABC中,∠BAC=90°,AB=5cm,AC=2cm,将△ABC绕顶点C按顺时针方向旋转45°至△A1B1C的位置,则线段AB扫过区域(图中的阴影部分)的面积为$\frac{25π}{8}$cm2.
如图,在△ABC中,∠BAC=90°,AB=5cm,AC=2cm,将△ABC绕顶点C按顺时针方向旋转45°至△A1B1C的位置,则线段AB扫过区域(图中的阴影部分)的面积为$\frac{25π}{8}$cm2.
分析 根据阴影部分的面积是:S扇形BCB1+S△CB1A1-S△ABC-S扇形CAA1,分别求得:扇形BCB1的面积,S△CB1A1,S△ABC以及扇形CAA1的面积,即可求解.
解答 解:在Rt△ABC中,BC=$\sqrt{A{B}^{2}+A{C}^{2}}$=$\sqrt{29}$cm,
扇形BCB1的面积是=$\frac{45π×(\sqrt{29})^{2}}{360}$=$\frac{29π}{8}$,
S△CB1A1=$\frac{1}{2}$×5×2=5;
S扇形CAA1=$\frac{45π×{2}^{2}}{360}$=$\frac{π}{2}$.
故S阴影部分=S扇形BCB1+S△CB1A1-S△ABC-S扇形CAA1
=$\frac{29π}{8}$+5-5-$\frac{π}{2}$
=$\frac{25π}{8}$.
故答案为:$\frac{25π}{8}$cm2.
点评 本题考查了旋转的性质,勾股定理,扇形的面积的计算,正确理解阴影部分的面积=S扇形BCB1+S△CB1A1-S△ABC-S扇形CAA1是关键.

练习册系列答案
相关题目
3.如果y=(a+1)x${\;}^{{a}^{2}}$是正比例函数,那么a的值是( )
| A. | -1 | B. | 0或1 | C. | -1或1 | D. | 1 |
18.下列命题中错误的是( )
| A. | 三角形的内心到这个三角形三边的距离相等 | |
| B. | 三角形的外心到这个三角形三个顶点的距离相等 | |
| C. | 三角形的重心到这个三角形三个顶点的距离相等 | |
| D. | 正三角形的垂心到这个三角形三边中点的距离相等 |

 B.
B.  C.
C.  D.
D.