题目内容
18．
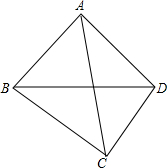在四边形ABCD中，AC=4，CD=3，∠ADB=∠ABD=∠ACD=45°，求BC．
分析 根据已知条件得到∠BAD=90°，A，B，C，D四点共圆，根据圆周角定理得到∠ACB=∠ADB=45°，由三角形的内角和得到∠BCD=90°，根据勾股定理于是得到结论．
解答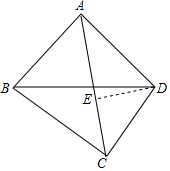 
解：过D作DE⊥AC于E，
∵∠ADB=∠ABD=∠ACD=45°，
∴∠BAD=90°，A，B，C，D四点共圆，
∴∠ACB=∠ADB=45°，
∴∠BCD=90°，
∵CD=3，
∴CE=DE=$\frac{3\sqrt{2}}{2}$，
∵AC=4，
∴AE=4-$\frac{3\sqrt{2}}{2}$，
∴AD=$\sqrt{A{E}^{2}+D{E}^{2}}$=25-12$\sqrt{2}$，
∴BD=$\sqrt{2}$AD=25$\sqrt{2}$-24，
∴BC=$\sqrt{B{D}^{2}-C{D}^{2}}$=$\sqrt{41-24\sqrt{2}}$=4$\sqrt{2}$-3．
点评 本题考查了等腰直角三角形的性质，四点共圆，勾股定理，余弦定理，熟练掌握余弦定理是解题的关键．
练习册系列答案
备战中考寒假系列答案
相关题目
8．在平面直角坐标系中，点（2，-1）关于原点对称的点的坐标是（ ）
| A． | （2，1） | B． | （-2，1） | C． | （-1，2） | D． | （-2，-1） |
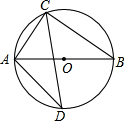己知：在⊙O中，直径AB的长为10cm，弦AC的长为6cm，∠ACB的平分线交⊙O于点D，
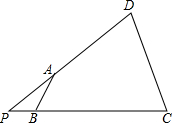如图，四边形ABCD中，∠ABC=∠DCB，DA，CB的延长线交于点P．
已知二次函数y=$\frac{1}{2}$x2+3x+2的图象与x轴交于A、B两点，与y轴交于D点，顶点为C，求四边形ACBD的面积．