题目内容
12.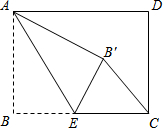 如图,矩形ABCD中,AB=3,BC=4,点E是BC边上一点,连接AE,把∠B沿AE折叠,使点B落在点B′处,当△CEB′为直角三角形时,求BE的长.
如图,矩形ABCD中,AB=3,BC=4,点E是BC边上一点,连接AE,把∠B沿AE折叠,使点B落在点B′处,当△CEB′为直角三角形时,求BE的长.
分析 分类讨论:当∠B′EC=90°时,如图,根据折叠性质得∠BEA=∠B′EA=45°,则BE=AB=3;当∠EB′C=90°时,如图,先利用勾股定理计算出AC=5,再根据折叠性质得∠B=∠AB′E=90°,EB=EB′,AB′=AB=3,于是可判断点A、B′、C共线,且CB′=AC-AB′=2,设BE=x,则EB′=x,CE=4-x,在Rt△CEB′中根据勾股定理得到x2+22=(4-x)2,解得x=$\frac{3}{2}$,即BE=$\frac{3}{2}$;∠ECB′不可能为90°.
解答 解:当∠B′EC=90°时,
如图,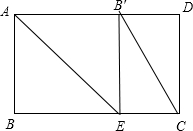
∴∠BEB′=90°,
∵矩形ABCD沿AE折叠,使点B落在点B′处,
∴∠BEA=∠B′EA=45°,
∴BE=AB=3;
当∠EB′C=90°时,
如图,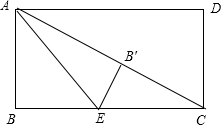
在Rt△ABC中,∵AB=3,BC=4,
∴AC=$\sqrt{A{B}^{2}+B{C}^{2}}$=5,
∵矩形ABCD沿AE折叠,使点B落在点B′处,
∴∠B=∠AB′E=90°,EB=EB′,AB′=AB=3,
∴点A、B′、C共线,即点B′在AC上,CB′=AC-AB′=5-3=2,
设BE=x,则EB′=x,CE=4-x,
在Rt△CEB′中,∵EB′2+CB′2=CE2,
∴x2+22=(4-x)2,解得x=$\frac{3}{2}$,
即BE=$\frac{3}{2}$,
综上所述,BE的长为3或$\frac{3}{2}$.
点评 本题考查了折叠的性质:折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.也考查了矩形的性质和勾股定理.

练习册系列答案
相关题目
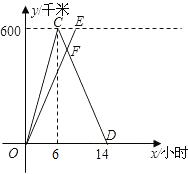 已知A、B两城相距600千米,甲、乙两车同时从A城出发驶向B城,甲车到达B城后立即沿原路返回,如图是它们离A城的距离y(千米)与行驶时间x(小时)之间的函数图象.
已知A、B两城相距600千米,甲、乙两车同时从A城出发驶向B城,甲车到达B城后立即沿原路返回,如图是它们离A城的距离y(千米)与行驶时间x(小时)之间的函数图象. 如图,画出四边形ABCD关于点O的对称图形.
如图,画出四边形ABCD关于点O的对称图形.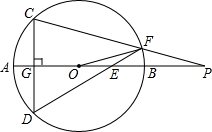 如图,已知AB是⊙O的直径,点E在线段AB上,CD⊥AB于G,连接DE交⊙O于F,连接CF交AB延长线于P.
如图,已知AB是⊙O的直径,点E在线段AB上,CD⊥AB于G,连接DE交⊙O于F,连接CF交AB延长线于P.