题目内容
14．
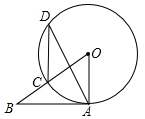如图，AB为⊙O的切线，切点为A，BO交⊙O于点C，点D在⊙O上，若∠ABO的度数是32°，则∠ADC的度数是（ ）| A． | 29° | B． | 30° | C． | 31° | D． | 32° |
分析 先根据切线的性质求出∠AOC的度数，再根据三角形内角和定理求出∠AOB的度数，由圆周角定理即可解答．
解答 解：∵AB切⊙O于点A，
∴OA⊥AB，
∵∠ABO=32°，
∴∠AOB=90°-32°=58°，
∴∠ADC=$\frac{1}{2}$∠AOB=$\frac{1}{2}$×58°=29°，
故选A．
点评 本题考查了圆的切线性质、圆心角和圆周的关系及解直角三角形的知识，熟记切线的性质是解题的关键．
练习册系列答案
相关题目
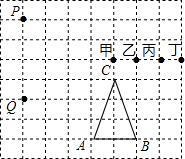如图，若A、B、C、P、Q、甲、乙、丙、丁都是方格纸中的格点，为使△PQR∽△ABC，则点R应是甲、乙、丙、丁四点中的（ ）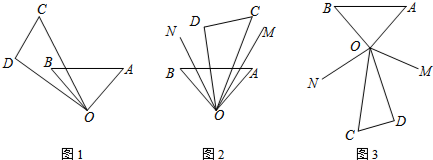
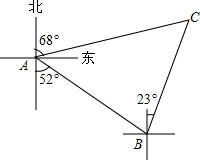如图，某轮船航行至A处测得灯塔C位于北偏东68°的方向上，若该轮船从A处以每小时18海里的速度沿南偏东52°方向匀速航行，1小时候到达码头B，此时测得灯塔C位于北偏东23°方向上．