题目内容
8.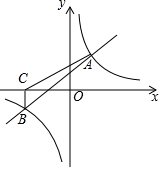 如图,一次函数y=x+2与反比例函数y=$\frac{k}{x}$的图象相交于A(2,m),B(-4,n)两点.
如图,一次函数y=x+2与反比例函数y=$\frac{k}{x}$的图象相交于A(2,m),B(-4,n)两点.(1)求反比例函数的解析式;
(2)根据所给条件,请直接写出不等式x+2>$\frac{k}{x}$的解集:-4<x<0或x>2;
(3)过点B作BC⊥x轴,垂足为C,连接AC,求S△ABC.
分析 (1)把函数图象上点的坐标代入解析式,计算即可;
(2)结合图象解答;
(3)求出点B的坐标,根据三角形面积公式计算.
解答 解:(1)把x=2,y=m代入y=x+2中,解得m=4,
∴点A坐标为(2,4),
∵点A在反比例函数y=$\frac{k}{x}$的图象上,
∴2=$\frac{k}{4}$,
解得,k=8,
则反比例函数的解析式为y=$\frac{8}{x}$;
(2)由图象可知,当-4<x<0或x>2时,x+2>$\frac{k}{x}$,
故答案为:-4<x<0或x>2;
(3)把x=-4,y=n代入y=x+2中,解得n=-2,
∴点B坐标为(-4,-2),
∴S△ABC=$\frac{1}{2}$×2×(2+4)=6.
点评 本题考查的是反比例函数与一次函数的交点问题,掌握函数图象上点的坐标特征、灵活运用数形结合思想是解题的关键.

练习册系列答案
相关题目
20.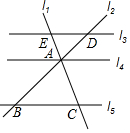 如图,l3∥l4∥l5,l1交l3,l4,l5于E,A,C,l2交l3,l4,l5于D,A,B,以下结论的错误的为( )
如图,l3∥l4∥l5,l1交l3,l4,l5于E,A,C,l2交l3,l4,l5于D,A,B,以下结论的错误的为( )
 如图,l3∥l4∥l5,l1交l3,l4,l5于E,A,C,l2交l3,l4,l5于D,A,B,以下结论的错误的为( )
如图,l3∥l4∥l5,l1交l3,l4,l5于E,A,C,l2交l3,l4,l5于D,A,B,以下结论的错误的为( )| A. | $\frac{EA}{AC}$=$\frac{DA}{AB}$ | B. | $\frac{BA}{BD}$=$\frac{CA}{CE}$ | C. | $\frac{CA}{CE}$=$\frac{DA}{DB}$ | D. | $\frac{EA}{EC}$=$\frac{DA}{DB}$ |
18.下列关于单项式$-\frac{{3x{y^2}}}{5}$的说法中,正确的是( )
| A. | 系数是3,次数是2 | B. | 系数是$-\frac{3}{5}$,次数是2 | ||
| C. | 系数是$\frac{3}{5}$,次数是3 | D. | 系数是$-\frac{3}{5}$,次数是3 |
 如图是每个面上都有一个汉字的正方体的表面展开图,那么在原正方体的表面上与汉字“爱”相对的面上的汉字是丽.
如图是每个面上都有一个汉字的正方体的表面展开图,那么在原正方体的表面上与汉字“爱”相对的面上的汉字是丽.
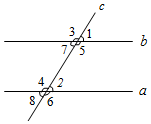 如图,直线a、b都与直线c相交,有下列条件:①∠1=∠2;②∠3+∠8=180°;③∠4=∠5;④∠6+∠7=180°.其中,能够判断a∥b的是( )
如图,直线a、b都与直线c相交,有下列条件:①∠1=∠2;②∠3+∠8=180°;③∠4=∠5;④∠6+∠7=180°.其中,能够判断a∥b的是( )