题目内容
19.阅读理解:大家知道:$\sqrt{2}$是无理数,而无理数是无限不循环小数,因此$\sqrt{2}$的小数部分我们不可能全部写出来,因为$\sqrt{2}$的整数部分是1,所以我们可以用$\sqrt{2}-1$来表示$\sqrt{2}$的小数部分.请你解答:已知:x是$10+\sqrt{3}$的整数部分,y是$10+\sqrt{3}$的小数部分,求x-y+$\sqrt{3}$的值.分析 根据11<10+$\sqrt{3}$<12,可得$10+\sqrt{3}$的整数部分和小数部分,再进一步求x-y+$\sqrt{3}$的值即可.
解答 解:∵11<10+$\sqrt{3}$<12,
∴x=11,y=$10+\sqrt{3}-11=\sqrt{3}-1$,
所以可得x-y+$\sqrt{3}$=11-$\sqrt{3}+1+\sqrt{3}$=12.
点评 此题考查估算无理数的大小,估算出10+$\sqrt{3}$的大小是解决问题的关键.

练习册系列答案
相关题目
14.一个整数加上-15,和大于0,这个整数可能是( )
| A. | 16.5 | B. | 16 | C. | 15 | D. | 14 |
 如图,在平面直角坐标系中,点A,B,C的坐标为(1,4),(5,4),(1,-2),则△ABC外接圆的圆心坐标是(3,1).
如图,在平面直角坐标系中,点A,B,C的坐标为(1,4),(5,4),(1,-2),则△ABC外接圆的圆心坐标是(3,1). 一辆货车从A地开往B地,一辆小汽车从B地开往A地.同时出发,都匀速行驶,各自到达终点后停止.设货车、小汽车之间的距离为s(千米),货车行驶的时间为t(小时),S与t之间的函数关系如图所示.下列说法中正确的有( )
一辆货车从A地开往B地,一辆小汽车从B地开往A地.同时出发,都匀速行驶,各自到达终点后停止.设货车、小汽车之间的距离为s(千米),货车行驶的时间为t(小时),S与t之间的函数关系如图所示.下列说法中正确的有( )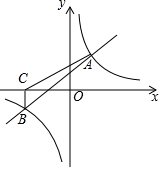 如图,一次函数y=x+2与反比例函数y=$\frac{k}{x}$的图象相交于A(2,m),B(-4,n)两点.
如图,一次函数y=x+2与反比例函数y=$\frac{k}{x}$的图象相交于A(2,m),B(-4,n)两点.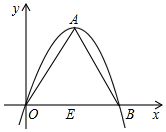 如果一条抛物线y=ax2+bx+c(a≠0)与x轴有两个交点,那么以该抛物线的顶点和这两个交点为顶点的三角形称为这条抛物线的“抛物线三角形”.
如果一条抛物线y=ax2+bx+c(a≠0)与x轴有两个交点,那么以该抛物线的顶点和这两个交点为顶点的三角形称为这条抛物线的“抛物线三角形”.