题目内容
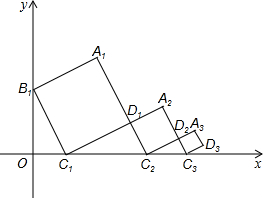 在平面直角坐标系中,正方形A1B1C1D1的位置如图所示,点B1的坐标为(0,2),点C1的坐标为(1,0),延长A1D1交x轴于点C2,作正方形D1C2D2A2,延长A2D2交x轴于点C3,作正方形D2C3D3A3,….按这样的规律进行下去,则点A5到x轴的距离是
在平面直角坐标系中,正方形A1B1C1D1的位置如图所示,点B1的坐标为(0,2),点C1的坐标为(1,0),延长A1D1交x轴于点C2,作正方形D1C2D2A2,延长A2D2交x轴于点C3,作正方形D2C3D3A3,….按这样的规律进行下去,则点A5到x轴的距离是考点:正方形的性质,坐标与图形性质
专题:规律型
分析:根据勾股定理可得正方形A1B1C1D1的边长为
=
,根据相似三角形的性质可得后面正方形的边长依次是前面正方形边长的
,依次得到第四个正方形和第五个正方形的边长,进一步得到点A5到x轴的距离.
| 22+12 |
| 5 |
| 1 |
| 2 |
解答: 解:在Rt△OB1C1中,OB1=2,OC1=1,
解:在Rt△OB1C1中,OB1=2,OC1=1,
正方形A1B1C1D1的边长为
=
,
∵∠B1OC1=∠C1D1C2=90°,∠1+∠2=∠2+∠3=90°,
∴∠1=∠3,
∴△B1OC1∽C1D1C2△,
∴D1C2=
,
依此可得D3C4=
,D4C5=
,
∴C4A5=
,
∴点A5到x轴的距离是
÷
=
.
故答案为:
.
 解:在Rt△OB1C1中,OB1=2,OC1=1,
解:在Rt△OB1C1中,OB1=2,OC1=1,正方形A1B1C1D1的边长为
| 22+12 |
| 5 |
∵∠B1OC1=∠C1D1C2=90°,∠1+∠2=∠2+∠3=90°,
∴∠1=∠3,
∴△B1OC1∽C1D1C2△,
∴D1C2=
| 1 |
| 2 |
| 5 |
依此可得D3C4=
| 1 |
| 8 |
| 5 |
| 1 |
| 16 |
| 5 |
∴C4A5=
| 3 |
| 16 |
| 5 |
∴点A5到x轴的距离是
| 3 |
| 16 |
| 5 |
| 5 |
| 3 |
| 16 |
故答案为:
| 3 |
| 16 |
点评:本题考查了正方形的性质,坐标与图形性质,求出第四个正方形和第五个正方形的边长是解题的关键.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目

 已知梯形ABCD,AB∥CD,∠D=2∠B,AD=10,AB=15,求CD的长.
已知梯形ABCD,AB∥CD,∠D=2∠B,AD=10,AB=15,求CD的长.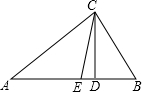 如图,CD、CE分别是△ABC的高和角平分线,∠A=30°,∠B=60°,则∠DCE=
如图,CD、CE分别是△ABC的高和角平分线,∠A=30°,∠B=60°,则∠DCE= 如图,在周长为10cm的?ABCD中,AB≠AD,AC、BD相交于点O,OE⊥BD交AD于点E,连接BE,则△ABE的周长为
如图,在周长为10cm的?ABCD中,AB≠AD,AC、BD相交于点O,OE⊥BD交AD于点E,连接BE,则△ABE的周长为