题目内容
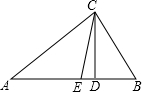 如图,CD、CE分别是△ABC的高和角平分线,∠A=30°,∠B=60°,则∠DCE=
如图,CD、CE分别是△ABC的高和角平分线,∠A=30°,∠B=60°,则∠DCE=考点:三角形内角和定理
专题:
分析:先根据三角形内角和定理计算出∠ACB=180°-∠A-∠B=90°,再根据三角形的高和角平分线的定义得到∠BCE=
∠ACB=45°,∠BDC=90°,于是可计算出∠BCD=30°,然后利用∠DCE=∠BCE-∠BCD进行计算即可.
| 1 |
| 2 |
解答:解:∵∠A=30°,∠B=60°,
∴∠ACB=180°-∠A-∠B=90°,
∵CD、CE分别是△ABC的高和角平分线,
∴∠BCE=
∠ACB=45°,∠BDC=90°,
∴∠BCD=90°-∠B=30°,
∴∠DCE=∠BCE-∠BCD=45°-30°=15°.
故答案为:15°.
∴∠ACB=180°-∠A-∠B=90°,
∵CD、CE分别是△ABC的高和角平分线,
∴∠BCE=
| 1 |
| 2 |
∴∠BCD=90°-∠B=30°,
∴∠DCE=∠BCE-∠BCD=45°-30°=15°.
故答案为:15°.
点评:本题考查了三角形内角和定理:三角形内角和是180°.

练习册系列答案
相关题目
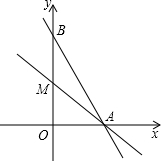 如图,在平面直角坐标系中,函数y=-2x+12的图象分别交x轴、y轴于A、B两点,过点A的直线交y 正半轴于点M,且点M为线段OB的中点.
如图,在平面直角坐标系中,函数y=-2x+12的图象分别交x轴、y轴于A、B两点,过点A的直线交y 正半轴于点M,且点M为线段OB的中点.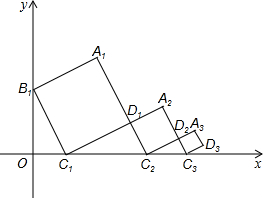 在平面直角坐标系中,正方形A1B1C1D1的位置如图所示,点B1的坐标为(0,2),点C1的坐标为(1,0),延长A1D1交x轴于点C2,作正方形D1C2D2A2,延长A2D2交x轴于点C3,作正方形D2C3D3A3,….按这样的规律进行下去,则点A5到x轴的距离是
在平面直角坐标系中,正方形A1B1C1D1的位置如图所示,点B1的坐标为(0,2),点C1的坐标为(1,0),延长A1D1交x轴于点C2,作正方形D1C2D2A2,延长A2D2交x轴于点C3,作正方形D2C3D3A3,….按这样的规律进行下去,则点A5到x轴的距离是