题目内容
(1)解方程:
+
=1.
(2)解分式方程:
+
=-1.
| x |
| x-1 |
| 1 |
| x2-1 |
(2)解分式方程:
| 2+x |
| 2-x |
| 16 |
| x2-4 |
考点:解分式方程
专题:计算题
分析:分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.
解答:解:(1)方程的两边同乘(x+1)(x-1),得x(x+1)+1=x2-1,
去括号得:x2+x+1=x2-1,
解得:x=-2,
检验:把x=-2代入(x+1)(x-1)=3≠0,
∴原方程的解为:x=-2;
(2)去分母得:-(x+2)2+16=4-x2,
去括号得:-x2-4x-4+16=4-x2,
解得:x=2,
经检验x=2是增根,分式方程无解.
去括号得:x2+x+1=x2-1,
解得:x=-2,
检验:把x=-2代入(x+1)(x-1)=3≠0,
∴原方程的解为:x=-2;
(2)去分母得:-(x+2)2+16=4-x2,
去括号得:-x2-4x-4+16=4-x2,
解得:x=2,
经检验x=2是增根,分式方程无解.
点评:此题考查了解分式方程,解分式方程的基本思想是“转化思想”,把分式方程转化为整式方程求解.解分式方程一定注意要验根.

练习册系列答案
相关题目
下列抛物线中,与y=-
x2+3x-5的开口方向大小相同,只是位置不同的是( )
| 1 |
| 2 |
A、y=-
| ||||||
| B、y=-x2+x-5 | ||||||
C、y=-
| ||||||
D、y=-
|
用反证法证明“若⊙O的半径为r,点P到圆心的距离d<r,则点P在⊙O的内部”首先应假设( )
| A、d≤r |
| B、d≥r |
| C、点P在⊙O的外部 |
| D、点P在⊙O上或点P在⊙O的外部 |
下列运算正确的是( )
| A、a0=0 |
| B、(2a2)3=6a6 |
| C、(a-1)2=a2-1 |
| D、2a+3a=5a |
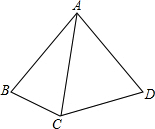 如图,AB=AC=AD,∠BAD=80°,则∠BCD的大小是
如图,AB=AC=AD,∠BAD=80°,则∠BCD的大小是 如图,AB∥CD,∠B=76°,∠F=30°,求∠D的度数.
如图,AB∥CD,∠B=76°,∠F=30°,求∠D的度数.