题目内容
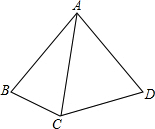 如图,AB=AC=AD,∠BAD=80°,则∠BCD的大小是
如图,AB=AC=AD,∠BAD=80°,则∠BCD的大小是考点:等腰三角形的性质
专题:
分析:在△ABC中可得∠BCA=
(180°-∠BAC),在△ACD中可得∠DCA=
(180°-∠CAD),结合条件,两式相加可求得∠BCD的大小.
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:∵AB=AC=AD,
∴∠BCA=∠B=
(180°-∠BAC),∠DCA=∠D=
(180°-∠CAD),
∴∠BCD=∠BCA+∠DCA=
(180°-∠BAC)+
(180°-∠CAD)=180°-
(∠BAC+∠CAD)=180°-
∠BAD=180°-40°=140°,
故答案为:140°.
∴∠BCA=∠B=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠BCD=∠BCA+∠DCA=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
故答案为:140°.
点评:本题主要考查等角三角形的性质及三角形内角和定理,掌握等边对等角和三角形内角和为180°是解题的关键.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案
相关题目
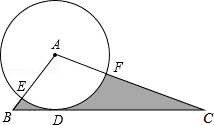 如图,在△ABC中,BC=4,以点A为圆心,2为半径的⊙A与BC相切于点D,交AB于点E,交AC于点F,且∠EAF=80°,则图中阴影部分的面积为( )
如图,在△ABC中,BC=4,以点A为圆心,2为半径的⊙A与BC相切于点D,交AB于点E,交AC于点F,且∠EAF=80°,则图中阴影部分的面积为( )| A、4 | ||
B、
| ||
C、4-
| ||
D、8-
|
下列图形对称轴最多的是( )
| A、正方形 | B、等边三角形 |
| C、等腰三角形 | D、线段 |
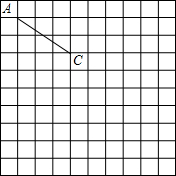 如图,在正方形网格中,每个小正方形的边长为1个单位长度,已知△ABC的顶点A、C的坐标分别为(-4,4)、(-1,2),点B坐标为(-2,1).
如图,在正方形网格中,每个小正方形的边长为1个单位长度,已知△ABC的顶点A、C的坐标分别为(-4,4)、(-1,2),点B坐标为(-2,1).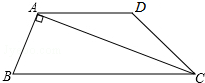 如图,在四边形ABCD中,AD∥BC,CA是∠BCD的平分线,且AB⊥AC,AB=4,AD=6,
如图,在四边形ABCD中,AD∥BC,CA是∠BCD的平分线,且AB⊥AC,AB=4,AD=6,