题目内容
1. 如图,在△ABC中,点A1、A2是AB的三等分点,点B1、B2是BC的三等分点,点C1、C2、C3、C4是AC的五等分点,记四边形A1A2C3C4、B1B2C1C2的面积分别为S1、S2,若S1+S2=12,则五边形A2BB1C2C3的面积为14.
如图,在△ABC中,点A1、A2是AB的三等分点,点B1、B2是BC的三等分点,点C1、C2、C3、C4是AC的五等分点,记四边形A1A2C3C4、B1B2C1C2的面积分别为S1、S2,若S1+S2=12,则五边形A2BB1C2C3的面积为14.
分析 如图.连结BC2,BC3.设a,b,c,d,e分别为其所在三角形的面积.由A1C4∥A2C3,AA1=A1A2,AC4=C4C3,推出△AA1C4∽△AA2C3,推出$\frac{a}{a+{S}_{1}}$=$\frac{1}{4}$,推出a=$\frac{1}{3}$S1,同理可证b=$\frac{1}{3}$S2,由S1+S2=12,推出a+b=4,由AA2=2BA2,推出d=$\frac{1}{2}$(a+S1),同理e=$\frac{1}{2}$(b+S2),推出d+e=$\frac{1}{2}$(a+S1+S2+b)=8,由此AC3=22C3,推出c=$\frac{1}{2}$(d+a+S1)=$\frac{1}{2}$(e+S2+b),推出2c=$\frac{1}{2}$(d+e+a+b+S1+S2)=12,即c=6,根据五边形A2BB1C2C3的面积=d+c+e即可解决问题.
解答 解:如图.连结BC2,BC3.设a,b,c,d,e分别为其所在三角形的面积.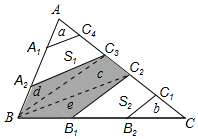
∵A1C4∥A2C3,AA1=A1A2,AC4=C4C3,
∴△AA1C4∽△AA2C3,
∴$\frac{a}{a+{S}_{1}}$=$\frac{1}{4}$,
∴$\frac{a}{{S}_{1}}$=$\frac{1}{3}$,
∴a=$\frac{1}{3}$S1,同理可证b=$\frac{1}{3}$S2,
∵S1+S2=12,
∴a+b=4,
∵AA2=2BA2,
∴d=$\frac{1}{2}$(a+S1),同理e=$\frac{1}{2}$(b+S2),
∴d+e=$\frac{1}{2}$(a+S1+S2+b)=8,
∵AC3=22C3,
∴c=$\frac{1}{2}$(d+a+S1)=$\frac{1}{2}$(e+S2+b),
∴2c=$\frac{1}{2}$(d+e+a+b+S1+S2)=12,
∴c=6,
∴五边形A2BB1C2C3的面积=c+d+e=14,
故答案为14.
点评 本题考查相似三角形的性质、三角形的面积等知识,解题的关键是学会利用参数解决问题,学会用整体的思想思考问题,掌握异底同高的三角形的面积比等于底的比,属于中考填空题中的压轴题.

 我市某工艺厂设计了一款成本为10元/件的工艺品投放市场进行试销,经过市场调查,得到如下数据:
我市某工艺厂设计了一款成本为10元/件的工艺品投放市场进行试销,经过市场调查,得到如下数据:| 销售单价x(元/件) | … | 20 | 30 | 40 | 50 | 60 | … |
| 每天销售量y(件) | … | 500 | 400 | 300 | 200 | 100 | … |
(2)若市物价部门规定,该工艺品销售单价最高不能超过35元/件,那么销售单价定为多少时,工艺厂试销该工艺品每天获得的利润最大?最大利润是多少?
 如图,△ABC中,若∠B=∠C,BD=CE,CD=BF,∠A=40°,则∠EDF=( )
如图,△ABC中,若∠B=∠C,BD=CE,CD=BF,∠A=40°,则∠EDF=( )| A. | 80° | B. | 45° | C. | 60° | D. | 70° |
 如图,△ABC中,AC=13,AB=12,BC=5,CD是△ABC的角平分线,DE⊥AC于E,连结EB.
如图,△ABC中,AC=13,AB=12,BC=5,CD是△ABC的角平分线,DE⊥AC于E,连结EB.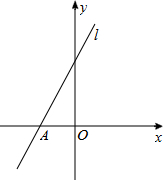 如右图,在直角坐标系中,点A(-4,0),直线l与x轴夹角为60°,点B在直线l上,且AB=10,求点B的坐标.
如右图,在直角坐标系中,点A(-4,0),直线l与x轴夹角为60°,点B在直线l上,且AB=10,求点B的坐标. 如图,在△ABC中,按以下步骤作图:
如图,在△ABC中,按以下步骤作图: 如图所示,有一块呈三角形的草坪,其一边长为20m,在这个草坪的图纸上,若这条边的长为5cm,其他两边的长都是3.5cm,则该草坪其他两边的实际长度为14m;14m.
如图所示,有一块呈三角形的草坪,其一边长为20m,在这个草坪的图纸上,若这条边的长为5cm,其他两边的长都是3.5cm,则该草坪其他两边的实际长度为14m;14m.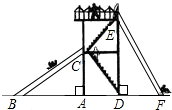 如图有两个长度相同的滑梯,左边滑梯的高度AC与右边滑梯水平方向的长度DF相等,若∠CBA=32°,求∠FED和∠EFD的度数.
如图有两个长度相同的滑梯,左边滑梯的高度AC与右边滑梯水平方向的长度DF相等,若∠CBA=32°,求∠FED和∠EFD的度数.