题目内容
12.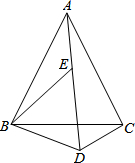 如图,已知△ABC和△BDE都是等边三角形,且A、E、D三点在同一直线上,试说明BD+CD=AD的理由.
如图,已知△ABC和△BDE都是等边三角形,且A、E、D三点在同一直线上,试说明BD+CD=AD的理由.
分析 首先证明△ABE≌△CBD,进而得到DC=AE,再由AD=AE+ED利用等量代换AD=BD+CD.
解答 证明:∵△ABC和△BDE都是等边三角形,
∴AB=AC,EB=DB=ED,∠ABC=∠EBD=60°,
∴∠ABC-∠EBC=∠EBD-∠EBC,
即∠ABE=∠CBD,
在△ABE和△CBD中,
$\left\{\begin{array}{l}{AB=BC}\\{∠ABE=∠CBD}\\{BD=BE}\end{array}\right.$,
∴△ABE≌△CBD(SAS),
∴DC=AE,
∵AD=AE+ED,
∴AD=BD+CD
点评 此题主要考查了全等三角形的判定与性质,关键是掌握全等三角形的判定与性质.

练习册系列答案
 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案
相关题目
7.如图所示,在餐桌上摆碗,一张餐桌上放6个碗,2张餐桌上放12个碗,按图继续排列餐桌并摆碗.

填写表格:

填写表格:
| 桌子的张数 | 1 | 2 | 3 | 4 | … | n |
| 摆碗数 | 6 | 12 | 18 | 24 | 6n |
4.关于x的一元二次方程a(x+3)2+3=0的解的情况是( )
| A. | 有两个不相等的实数根 | B. | 有两个相等的实数根 | ||
| C. | 没有实数根 | D. | 无法确定 |
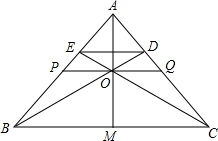 如图,已知:△ABC中,M为BC边的中点,O为AM上一点,BO的延长线交AC于点D,CO延长线交AB于点E,PQ∥BC,且PQ过点O与AB、AC分别交于P和点Q,求证:
如图,已知:△ABC中,M为BC边的中点,O为AM上一点,BO的延长线交AC于点D,CO延长线交AB于点E,PQ∥BC,且PQ过点O与AB、AC分别交于P和点Q,求证: