题目内容
2.已知二次函数y=x2-2mx+4m-8,当x≤2时,y随x的增大而减小,则m的取值范围是m≥2.分析 先根据二次函数的解析式判断出函数的开口方向,再由当x≤2时,函数值y随x的增大而减小可知二次函数的对称轴x=-$\frac{b}{2a}$≥2,故可得出关于m的不等式,求出m的取值范围即可.
解答 解:∵二次函数y=x2-2mx+4m-8,a=1>0,
∴抛物线开口向上,
∵当x≤2时,函数值y随x的增大而减小,
∴二次函数的对称轴x=-$\frac{b}{2a}$≥2,即-$\frac{-2m}{2}$≥2,
解得m≥2.
故答案为:m≥2.
点评 本题考查的是二次函数的性质,熟知二次函数的增减性是解答此题的关键.

练习册系列答案
相关题目
13.某地杨梅丰收,准备将已经采摘下来的11400公斤杨梅运送杭州,现有甲、乙、丙三种车型共选择,每辆车运载能力和运费如表表示(假设每辆车均满载)
(1)若全部杨梅都用甲、乙两种车型来运,需运费8700元,则需甲、乙两种车型各几辆?
(2)为了节省运费,现打算用甲、乙、丙三种车型都参与运送,已知它们的总辆数为15辆,你能分别求出这三种车型的辆数吗?怎样安排运费最省?
| 车型 | 甲 | 乙 | 丙 |
| 汽车运载量(公斤/辆) | 600 | 800 | 900 |
| 汽车运费(元/辆) | 500 | 600 | 700 |
(2)为了节省运费,现打算用甲、乙、丙三种车型都参与运送,已知它们的总辆数为15辆,你能分别求出这三种车型的辆数吗?怎样安排运费最省?
7.下列方程是一元二次方程的是( )
| A. | $2{x^2}-\frac{3}{x}=1$ | B. | x2=0 | C. | (2x+1)(2x-1)=4x(x+7) | D. | x(x2-5)=5 |
14.若|a-1|+(b+2)2=0,则b-a-$\frac{1}{2}$的值是( )
| A. | $-3\frac{1}{2}$ | B. | $-2\frac{1}{2}$ | C. | $-1\frac{1}{2}$ | D. | $1\frac{1}{2}$ |
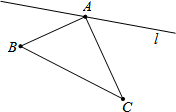 如图,∠BAC=90°,AB=22,AC=28.点P从B点出发沿B→A→C路径向终点C运动;点Q从C点出发沿C→A→B路径向终点B运动.点P和Q分别以每秒2和3个单位的速度同时开始运动,只要有一点到达相应的终点时两点同时停止运动;在运动过程中,分别过P和Q作PF⊥l于F,QG⊥l于G.问:点P运动多少秒时,△PFA与△QAG全等?
如图,∠BAC=90°,AB=22,AC=28.点P从B点出发沿B→A→C路径向终点C运动;点Q从C点出发沿C→A→B路径向终点B运动.点P和Q分别以每秒2和3个单位的速度同时开始运动,只要有一点到达相应的终点时两点同时停止运动;在运动过程中,分别过P和Q作PF⊥l于F,QG⊥l于G.问:点P运动多少秒时,△PFA与△QAG全等? 如图,从镜子中看到一钟表的时针和分针,此时的实际时刻是8:00.
如图,从镜子中看到一钟表的时针和分针,此时的实际时刻是8:00.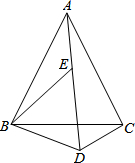 如图,已知△ABC和△BDE都是等边三角形,且A、E、D三点在同一直线上,试说明BD+CD=AD的理由.
如图,已知△ABC和△BDE都是等边三角形,且A、E、D三点在同一直线上,试说明BD+CD=AD的理由.