题目内容
16. 如图,D是BC上一点,E是AB上一点,AD、CE交于点P,且AE:EB=3:2,CP:CE=5:6,那么DB:CD=( )
如图,D是BC上一点,E是AB上一点,AD、CE交于点P,且AE:EB=3:2,CP:CE=5:6,那么DB:CD=( )| A. | 1:2 | B. | 1:3 | C. | 2:3 | D. | 1:4 |
分析 作EF∥BC交AD于F,如图,根据平行线分线段成比例定理,由EF∥BD得到EF:BD=AE:AB=3:5,则BD=$\frac{5}{3}$EF,由EF∥CD得到EF:CD=1:5,则CD=5EF,然后计算BD:CD.
解答 解:作EF∥BC交AD于F,如图,
∵EF∥BD,AE:EB=3:2,
∴EF:BD=AE:AB=3:5,
∴BD=$\frac{5}{3}$EF,
∵EF∥CD,
∴EF:CD=EP:PC,
而CP:CE=5:6,
∴EF:CD=1:5,
∴CD=5EF,
∴BD:CD=$\frac{5}{3}$EF:5EF=1:3.
故选B.
点评 本题考查了平行线分线段成比例:三条平行线截两条直线,所得的对应线段成比例.

练习册系列答案
相关题目
1.下列计算正确的是( )
| A. | 4x2-x2=4 | B. | 2x2+3x2=5x5 | C. | 3xy-2xy=xy | D. | x+y=xy |
 如图,已知O为直线AD上一点,OB是∠AOC内部一条射线且满足∠AOB与∠AOC互补,OM、ON分别为∠AOC、∠AOB的平分线.
如图,已知O为直线AD上一点,OB是∠AOC内部一条射线且满足∠AOB与∠AOC互补,OM、ON分别为∠AOC、∠AOB的平分线.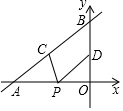 如图,直线y=$\frac{2}{3}$x+4与x轴、y轴分别交于点A和点B,点C、D分别为线段AB、OB的中点,点P为OA上一动点,PC+PD值最小时点P的坐标为(-$\frac{3}{2}$,0).
如图,直线y=$\frac{2}{3}$x+4与x轴、y轴分别交于点A和点B,点C、D分别为线段AB、OB的中点,点P为OA上一动点,PC+PD值最小时点P的坐标为(-$\frac{3}{2}$,0).