题目内容
17. 如图,将△ABC沿DE折叠,使点A与BC边的中点F重合,有下面四个结论:
如图,将△ABC沿DE折叠,使点A与BC边的中点F重合,有下面四个结论:(1)EF∥AB且EF=$\frac{1}{2}$AB;(2)AF平分∠DFE
(3)S四边形ADFE=$\frac{1}{2}$AF•DE;(4)∠BDF+∠FEC=2∠BAC.
其中一定成立的结论有(3)、(4).
分析 如图,运用翻折变换的性质证明AF⊥DE,∠EAF=∠EFA(设为α),∠FAD=∠AFD(设为β);借助三角形外角的性质可以判断选项(4)成立.运用对角线垂直的四边形的面积公式,可以判断选项(3)成立.
解答  解:如图,由翻折变换的性质得:AF⊥DE,且AO=FO;
解:如图,由翻折变换的性质得:AF⊥DE,且AO=FO;
∴EA=EF,DA=DF;
∴∠EAF=∠EFA(设为α),∠FAD=∠AFD(设为β),
∴∠BDF+∠FEC=2β+2α=2(α+β),而∠BAC=α+β,
∴∠BDF+∠FEC=2∠BAC,
故选项(4)成立.
∵AF⊥DE,
∴S四边形ADFE=$\frac{1}{2}$AF•DE,
故选项(3)成立.
故答案为(3)、(4).
点评 该题主要考查了翻折变换的性质、等腰三角形的性质、三角形外角的性质等几何知识点及其应用问题;牢固掌握翻折变换的性质等几何知识点是解题的基础和关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
8.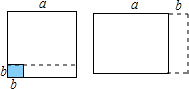 如图,在边长为a的正方形中挖掉一个边长为b的小正方形(a>b),把余下的部分剪拼成一个矩形.通过计算这两个图形的面积验证了一个等式,这个等式是( )
如图,在边长为a的正方形中挖掉一个边长为b的小正方形(a>b),把余下的部分剪拼成一个矩形.通过计算这两个图形的面积验证了一个等式,这个等式是( )
 如图,在边长为a的正方形中挖掉一个边长为b的小正方形(a>b),把余下的部分剪拼成一个矩形.通过计算这两个图形的面积验证了一个等式,这个等式是( )
如图,在边长为a的正方形中挖掉一个边长为b的小正方形(a>b),把余下的部分剪拼成一个矩形.通过计算这两个图形的面积验证了一个等式,这个等式是( )| A. | (a+2b)(a-b)=a2+ab-2b2 | B. | (a+b)2=a2+2ab+b2 | ||
| C. | a2-b2=(a+b)(a-b) | D. | (a-b)2=a2-2ab-b2. |
2.记录一天气温的变化情况,选用比较合适的统计图是( )
| A. | 条形统计图 | B. | 扇形统计图 | C. | 折线统计图 | D. | 都不可以 |

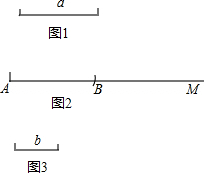 阅读材料:用尺规作图要求作线段AB等于线段a时,小明的具体作法如下:
阅读材料:用尺规作图要求作线段AB等于线段a时,小明的具体作法如下: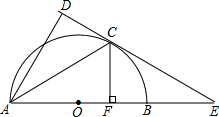 如图,AB为半圆的直径,O为圆心,C为圆弧上一点,AD垂直于过C点的切线,垂足为D,AB的延长线交直线CD于点E.
如图,AB为半圆的直径,O为圆心,C为圆弧上一点,AD垂直于过C点的切线,垂足为D,AB的延长线交直线CD于点E.