Question

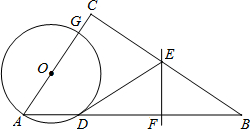如图，△ABC中，∠C=90°，点G是线段AC上的一动点（点G不与A、C重合），以AG为直径的⊙O交AB于点D，直线EF垂直平分BD，垂足为F，EF交BC于点E，连结DE．
（1）求证：DE是⊙O的切线；
（2）若cosA=

1

2

，AB=8

3

，AG=2

3

，求BE的长；
（3）若cosA=

1

2

，AB=8

3

，直接写出线段BE的取值范围．

Answer 1

考点：切线的判定,解直角三角形

专题：证明题,几何综合题

分析：（1）连接OD，根据互余得∠A+∠B=90°，再根据线段垂直平分线的性质得ED=EB，则∠B=∠EDB，加上∠A=∠ODA，所以∠ODA+∠EDB=90°，利用平角的定义得∠ODE=90°，然后根据切线的判定定理得到DE是⊙O的切线；
（2）连接GD，根据圆周角定理由AG为直径得∠ADG=90°，再根据特殊角的三角函数值得∠A=60°，则∠AGD=30°，根据含30度的直角三角形三边的关系，得AD=

1

2

AG=

3

，则BD=AB-AD=7

3

，所以BF=

1

2

BD=

7 3

2

，在Rt△BEF中，可计算出EF=

3

3

BF=

7

2

，BE=2EF=7；
（3）由于∠A=60°，则∠B=30°，所以AC=

1

2

AB=4

3

，由（2）得AD=

1

2

AG，所以BF=

1

2

（AB-AD）=4

3

-

1

4

AG，在Rt△BEF中，EF=

3

3

BF，BE=2EF=

2 3

3

BF=

2 3

3

（4

3

-

1

4

AG）=8-

3

6

AG，利用0＜AG＜AC即可得到6＜BE＜8．

解答：（1）证明：连接OD，如图，
∵△ABC中，∠C=90°，
∴∠A+∠B=90°，
∵直线EF垂直平分BD，
∴ED=EB，
∴∠B=∠EDB，
∵OA=OD，
∴∠A=∠ODA，
∴∠ODA+∠EDB=90°，
∴∠ODE=90°，
∴OD⊥DE，
∴DE是⊙O的切线；

（2）解：连接GD，
∵AG为直径，
∴∠ADG=90°，
∵cosA=

1

2

，
∴∠A=60°，
∴∠AGD=30°，
∴AD=

1

2

AG=

3

，
∵AB=8

3

，
∴BD=AB-AD=8

3

-

3

=7

3

，
∵直线EF垂直平分BD，
∴BF=

1

2

BD=

7 3

2

，
在Rt△BEF中，∠B=30°，
∴EF=

3

3

BF=

7

2

，
∴BE=2EF=7；

（3）解：∵cosA=

1

2

，
∴∠A=60°，
∴∠B=30°，
∴AC=

1

2

AB=4

3

，
由（2）得AD=

1

2

AG，
BF=

1

2

（AB-AD）=4

3

-

1

4

AG，
在Rt△BEF中，∠B=30°，
∴EF=

3

3

BF，
∴BE=2EF=

2 3

3

BF=

2 3

3

（4

3

-

1

4

AG）=8-

3

6

AG，
∵0＜AG＜AC，即0＜AG＜4

3

，
∴6＜BE＜8．

点评：本题考查了切线的判定定理：经过半径的外端且垂直于这条半径的直线是圆的切线．也考查了线段垂直平分线的性质和含30度的直角三角形三边的关系．