题目内容
 将?OABC放置在平面直角坐标系xOy内,已知AB边所在直线的函数解析式为:y=-x+4.若将?OABC绕点O逆时针旋转90°得OBDE,BD交OC于点P.
将?OABC放置在平面直角坐标系xOy内,已知AB边所在直线的函数解析式为:y=-x+4.若将?OABC绕点O逆时针旋转90°得OBDE,BD交OC于点P.(1)直接写出点C的坐标是
(2)求△OBP的面积;
(3)若再将四边形OBDE沿y轴正方向平移,设平移的距离为x(0≤x≤8),与?OABC重叠部分周长为L,试求出L关于x的函数关系式.
考点:一次函数综合题
专题:综合题
分析:(1)由AB边所在直线的解析为:y=-x+4,即可求得点A与B的坐标,又由四边形OABC是平行四边形,即可求得BC=OA=4,则可求得点C的坐标;
(2)易证得△OBP是等腰直角三角形,又由BO=4,即可求得△OBP的面积;
(3)分别从当0≤x<4时与当4≤x≤8时,利用等腰直角三角形的性质及平移的性质即可求得答案.
(2)易证得△OBP是等腰直角三角形,又由BO=4,即可求得△OBP的面积;
(3)分别从当0≤x<4时与当4≤x≤8时,利用等腰直角三角形的性质及平移的性质即可求得答案.
解答:解:(1)∵AB边所在直线的解析为:y=-x+4,
∴点A的坐标为:(4,0),点B的坐标为:(0,4),
∵四边形ABCD是平行四边形,
∴BC=OA=4,BC∥OA,
∴点C的坐标为:(-4,4);
故答案为:(-4,4);
(2)由旋转的性质,可得:OD=OB=4,
∵∠BOD=90°,
∴∠OBD=45°,
∵OB=BC,∠OBC=90°,
∴∠BOC=45°,
∴∠OPB=90°,BP=OP,
∵OB=4,
∴OP=BP=2
,
∴S△OBP=
OP•BP=4;
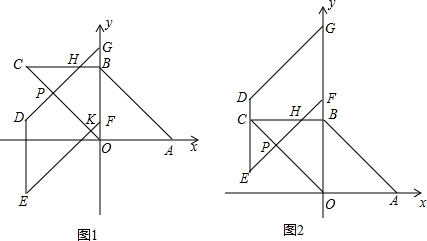
(3)分两种情况考虑:
①当0≤x≤4时,如图1所示,可得△CPH,△HBG与△FKO都为等腰直角三角形,
∴GB=OF,PH=PC,KF=OK,
此时重合部分五边形PHBFK的周长L=BH+HP+PK+KF+BF=GB+CP+PK+KO=BF=OC+FG=OC+OB=4+4
;
②当4≤x≤8时,如图2所示,此时△CPH与△BHF都为等腰直角三角形,
∴FB=HB=BG-GF=x-4,CH=CB-HB=4-(x-4)=8-x,CP=PH=
(8-x),
此时重合部分△CHP的周长L=CH+CP+PH=8-x+2×
(8-x)=8+8
-
x-x,
综上,L=
.
∴点A的坐标为:(4,0),点B的坐标为:(0,4),
∵四边形ABCD是平行四边形,
∴BC=OA=4,BC∥OA,
∴点C的坐标为:(-4,4);
故答案为:(-4,4);
(2)由旋转的性质,可得:OD=OB=4,
∵∠BOD=90°,
∴∠OBD=45°,
∵OB=BC,∠OBC=90°,
∴∠BOC=45°,
∴∠OPB=90°,BP=OP,
∵OB=4,
∴OP=BP=2
| 2 |
∴S△OBP=
| 1 |
| 2 |

(3)分两种情况考虑:
①当0≤x≤4时,如图1所示,可得△CPH,△HBG与△FKO都为等腰直角三角形,
∴GB=OF,PH=PC,KF=OK,
此时重合部分五边形PHBFK的周长L=BH+HP+PK+KF+BF=GB+CP+PK+KO=BF=OC+FG=OC+OB=4+4
| 2 |
②当4≤x≤8时,如图2所示,此时△CPH与△BHF都为等腰直角三角形,
∴FB=HB=BG-GF=x-4,CH=CB-HB=4-(x-4)=8-x,CP=PH=
| ||
| 2 |
此时重合部分△CHP的周长L=CH+CP+PH=8-x+2×
| ||
| 2 |
| 2 |
| 2 |
综上,L=
|
点评:此题属于一次函数综合题,涉及的知识有:等腰三角形的判定与性质,坐标与图形性质,勾股定理,以及平移的性质,熟练掌握性质及定理是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
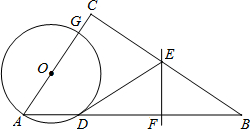 如图,△ABC中,∠C=90°,点G是线段AC上的一动点(点G不与A、C重合),以AG为直径的⊙O交AB于点D,直线EF垂直平分BD,垂足为F,EF交BC于点E,连结DE.
如图,△ABC中,∠C=90°,点G是线段AC上的一动点(点G不与A、C重合),以AG为直径的⊙O交AB于点D,直线EF垂直平分BD,垂足为F,EF交BC于点E,连结DE. 如图,在⊙O中,∠AOB=60°,则∠ACB=
如图,在⊙O中,∠AOB=60°,则∠ACB= 如图,点C在线段AB上,其中AB=5cm,BC=2cm,则AC=
如图,点C在线段AB上,其中AB=5cm,BC=2cm,则AC=