题目内容
20.关于x的方程(k-1)x2-2kx+k+1=0.(1)求k为何值时,方程有两个不相等的实数根;
(2)求k为何值时,方程两个实数根中,一根是另一根的3倍.
分析 (1)由关于x的方程(k-1)x2-2kx+k+1=0有两个不相等的实数根,联立根的判别式>0及二次项系数非0可得出关于k的一元二次不等式组,解不等式组即可得出k的取值范围;
(2)由方程的求根公式表示出两个根,结合一根是另一根的3倍得出关于k的一元一次方程,解方程即可得出结论.
解答 解:(1)∵方程有两个不相等的实数根,
∴$\left\{\begin{array}{l}{k-1≠0}\\{{b}^{2}-4ac>0}\end{array}\right.$,即$\left\{\begin{array}{l}{k-1≠0}\\{(-2k)^{2}-4(k-1)(k+1)>0}\end{array}\right.$,
解得:k≠1.
∴当k≠1时,方程有两个不相等的实数很;
(2)(k-1)x2-2kx+k+1=0,
解得:x1=$\frac{-b-\sqrt{{b}^{2}-4ac}}{2a}$=1,x2=$\frac{-b+\sqrt{{b}^{2}-4ac}}{2a}$=$\frac{k+1}{k-1}$.
∵方程两个实数根中,一根是另一根的3倍,
∴$\frac{k+1}{k-1}$=3,或者$\frac{k+1}{k-1}$=$\frac{1}{3}$,
解得:k=2,或k=-2.
∴当k为-2或2时,方程两个实数根中,一根是另一根的3倍.
点评 本题考查了根的判别式、解一元一次方程、解一元二次不等式组以及求根公式,解题的关键是:(1)找出关于k的一元二次不等式组;(2)由求根公式表示出来两根.本题属于基础题,难度不大,解决该题型题目时,结合根的判别式以及二次项系数非0得出不等式组是关键.

练习册系列答案
相关题目
11.下列命题:①相等的角是对顶角;②若a∥b,b⊥c,则a⊥c;③同位角相等;④邻补角的平分线互相垂直.其中正确的有( )
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
5.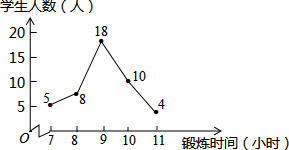 某班体育委员统计了全班45名同学一周的体育锻炼时间,并绘制了如图所示的折线统计图,则在体育锻炼时间这组数据中,众数和中位数分别是( )
某班体育委员统计了全班45名同学一周的体育锻炼时间,并绘制了如图所示的折线统计图,则在体育锻炼时间这组数据中,众数和中位数分别是( )
 某班体育委员统计了全班45名同学一周的体育锻炼时间,并绘制了如图所示的折线统计图,则在体育锻炼时间这组数据中,众数和中位数分别是( )
某班体育委员统计了全班45名同学一周的体育锻炼时间,并绘制了如图所示的折线统计图,则在体育锻炼时间这组数据中,众数和中位数分别是( )| A. | 18,18 | B. | 9,9 | C. | 9,10 | D. | 18,9 |
12.使式子$\sqrt{1-a}$有意义的a的范围是( )
| A. | a≥0 | B. | a≤0 | C. | a≥1 | D. | a≤1 |
9.已知一个正n边形的一个内角是它外角的5倍,则n等于( )
| A. | 8 | B. | 10 | C. | 12 | D. | 14 |
 解不等式组$\left\{\begin{array}{l}{2(x-2)≤3(x-1)}\\{\frac{x}{3}<\frac{x+1}{4}}\end{array}\right.$,并把它的解集表示在数轴上.
解不等式组$\left\{\begin{array}{l}{2(x-2)≤3(x-1)}\\{\frac{x}{3}<\frac{x+1}{4}}\end{array}\right.$,并把它的解集表示在数轴上.