题目内容
2.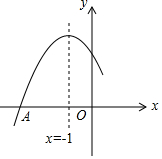 如图是抛物线y=ax2+bx+c(a≠0)的部分示意图,其中A点坐标(-3,0),对称轴是直线x=-1.下列四个结论:①2a=b;②abc>0;③若点B(-2,y1),C(-$\frac{5}{2}$,y2)为图象上两点,则y1<y2;④图象与x轴的另一个交点坐标为(1,0),其中正确的个数是( )
如图是抛物线y=ax2+bx+c(a≠0)的部分示意图,其中A点坐标(-3,0),对称轴是直线x=-1.下列四个结论:①2a=b;②abc>0;③若点B(-2,y1),C(-$\frac{5}{2}$,y2)为图象上两点,则y1<y2;④图象与x轴的另一个交点坐标为(1,0),其中正确的个数是( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 由于抛物线的对称轴为直线x=-$\frac{b}{2a}$=-1,则可对①进行判断;由抛物线开口方向得到a<0,由b=2a得到b<0,由抛物线与y轴交点在x轴上方得到c>0,则可对②进行判断;根据二次函数的性质,通过比较点B和点C到对称轴的距离的大小可对③进行判断;利用对称性可对④进行判断.
解答 解:∵抛物线的对称轴为直线x=-$\frac{b}{2a}$=-1,
∴b=2a,所以①正确;
∵抛物线开口向下,
∴a<0,
∴b=2a<0,
∵抛物线与y轴交点在x轴上方,
∴c>0,
∴abc>0,所以②正确;
∵B(-2,y1)到直线x=-1的距离比点C(-$\frac{5}{2}$,y2)到直线x=-1的距离小,
∴y1>y2,所以③错误;
∵抛物线与x的一个交点A点的坐标为(-3,0),而对称轴是直线x=-1,
∴抛物线与x轴的另一个交点坐标为(1,0),所以④正确.
故选C.
点评 本题考查了抛物线与x轴的交点:把求二次函数y=ax2+bx+c(a,b,c是常数,a≠0)与x轴的交点坐标问题转化为解关于x的一元二次方程.也考查了二次函数图象与系数的关系.

练习册系列答案
相关题目
12.王老师坚持绿色出行,每天先步行到离家500米的公共自行车点取车,然后骑车4.5千米到校.某天王老师从手机获知,骑车平均每小时比步行多10千米,共用时24分钟.设步行的平均速度为每小时x千米,则可列方程( )
| A. | $\frac{500}{x}$+$\frac{45}{x+10}$=24 | B. | $\frac{0.5}{x}$+$\frac{4.5}{x+10}$=$\frac{24}{60}$ | ||
| C. | $\frac{500}{x-10}$+$\frac{4500}{x}$=24 | D. | $\frac{0.5}{x-10}$+$\frac{4.5}{x}$=$\frac{24}{60}$ |
13.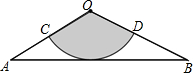 如图,从一张腰长为60cm,顶角为120°的等腰三角形铁皮OAB中剪出一个最大扇形OCD,用剪下的扇形铁皮围成一个圆锥的侧面(不计损耗),则该圆锥的高为( )
如图,从一张腰长为60cm,顶角为120°的等腰三角形铁皮OAB中剪出一个最大扇形OCD,用剪下的扇形铁皮围成一个圆锥的侧面(不计损耗),则该圆锥的高为( )
 如图,从一张腰长为60cm,顶角为120°的等腰三角形铁皮OAB中剪出一个最大扇形OCD,用剪下的扇形铁皮围成一个圆锥的侧面(不计损耗),则该圆锥的高为( )
如图,从一张腰长为60cm,顶角为120°的等腰三角形铁皮OAB中剪出一个最大扇形OCD,用剪下的扇形铁皮围成一个圆锥的侧面(不计损耗),则该圆锥的高为( )| A. | 10 cm | B. | 15 cm | C. | 10$\sqrt{3}$ cm | D. | 20$\sqrt{2}$ cm |
10. 如图,下列条件中,能判定a∥b的是( )
如图,下列条件中,能判定a∥b的是( )
 如图,下列条件中,能判定a∥b的是( )
如图,下列条件中,能判定a∥b的是( )| A. | ∠1=∠2 | B. | ∠1=∠4 | C. | ∠1+∠3=180° | D. | ∠3+∠4=180° |
17.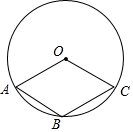 如图,点A,B,C均在圆O上,并且四边形OABC是菱形,那么∠O与2∠A的关系是( )
如图,点A,B,C均在圆O上,并且四边形OABC是菱形,那么∠O与2∠A的关系是( )
 如图,点A,B,C均在圆O上,并且四边形OABC是菱形,那么∠O与2∠A的关系是( )
如图,点A,B,C均在圆O上,并且四边形OABC是菱形,那么∠O与2∠A的关系是( )| A. | ∠O>2∠A | B. | ∠O=2∠A | C. | ∠O<2∠A | D. | 不能确定 |
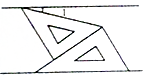 如图,将一副三角板和一张对边平行的纸条按下列方式摆放,两个三角板的一直角边重合,含30°角的直角三角板的斜边与纸条一边重合,含45°角的三角板的一个顶点在纸条的另一边上,则∠1的度数是( )
如图,将一副三角板和一张对边平行的纸条按下列方式摆放,两个三角板的一直角边重合,含30°角的直角三角板的斜边与纸条一边重合,含45°角的三角板的一个顶点在纸条的另一边上,则∠1的度数是( ) 如图,已知l1∥l2,直线l与l1、l2相交于C、D两点,把一块含30°角的三角尺按如图位置摆放.若∠1=130°,则∠2=20°.
如图,已知l1∥l2,直线l与l1、l2相交于C、D两点,把一块含30°角的三角尺按如图位置摆放.若∠1=130°,则∠2=20°. 如图是利用直尺和三角板过已知直线l外一点P作直线l的平行线的方法,其理由是同位角相等,两直线平行.
如图是利用直尺和三角板过已知直线l外一点P作直线l的平行线的方法,其理由是同位角相等,两直线平行.