题目内容
12. 如图,点A、B分别表示的数是6、-12,M、N、P为数轴上三个动点,它们同时都向右运动.点M从点A出发,速度为每秒2个单位长度,点N从点B出发,速度为点M的3倍,点P从原点出发,速度为每秒1个单位长度.
如图,点A、B分别表示的数是6、-12,M、N、P为数轴上三个动点,它们同时都向右运动.点M从点A出发,速度为每秒2个单位长度,点N从点B出发,速度为点M的3倍,点P从原点出发,速度为每秒1个单位长度.(1)当运动3秒时,点M、N、P分别表示的数是12、6、3;
(2)求运动多少秒时,点P到点M、N的距离相等?
分析 (1)用含时间t的算式表示出M、N、P分别表示的数,套入时间即可求得;
(2)N的速度快P的速度慢,可知点P到点M、N的距离相等分两种情况,分类探讨即可.
解答 解:设运动时间为t,根据题意可知:
M表示6+2t,N表示-12+6t,P表示t,
(1)将t=3代入M、N、P中,可得:
M表示12,N表示6,P表示3,
故答案为:12、6、3.
(2)由运动速度的快慢可知分两种情况:
①P是MN的中点,则t-(-12+6t)=6+2t-t,
解得t=1.
②点M、N重合,则-12+6t=6+2t,
解得t=$\frac{9}{2}$.
答:运动1或$\frac{9}{2}$秒后,点P到点M、N的距离相等.
点评 本题考查的一元一次方程的应用,解题的关键是借用一次函数的思想,设时间为t根据题意列出关系式即可求得.

练习册系列答案
 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案
相关题目
3.若单项式3x2y和$-\frac{1}{3}{x^{3a-4}}y$是同类项,则a的值是( )
| A. | $-\frac{2}{3}$ | B. | -2 | C. | 2 | D. | $\frac{2}{3}$ |
2.(-$\frac{1}{2}$)2001(-2)2000(-1)1999的正确答案( )
| A. | -$\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | 1 | D. | -1 |
 如图,由射线AB,BC,CD,DA组成平面图形,则∠1+∠2+∠3+∠4=360°.
如图,由射线AB,BC,CD,DA组成平面图形,则∠1+∠2+∠3+∠4=360°.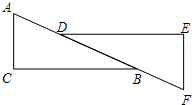 如图,在△ABC与△FDE中,点D在AB上,点B在DF上,∠C=∠E,AC∥FE,AD=FB.求证:△ABC≌△FDE.
如图,在△ABC与△FDE中,点D在AB上,点B在DF上,∠C=∠E,AC∥FE,AD=FB.求证:△ABC≌△FDE.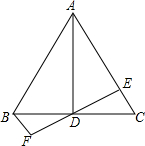 如图,在△ABC中,AB=AC,AD平分∠BAC,DE⊥AC于点E,BF⊥DE于点F
如图,在△ABC中,AB=AC,AD平分∠BAC,DE⊥AC于点E,BF⊥DE于点F 如图1,已知GF∥BC.
如图1,已知GF∥BC.