题目内容
阅读下面材料:
小凯遇到这样一个问题:如图1,在四边形ABCD中,对角线AC、BD相交于点O,
AC=4,BD=6,∠AOB=30°,求四边形ABCD的面积.
小凯发现,分别过点A、C作直线BD的垂线,垂足分别为点E、F,设AO为m,通过计算△ABD与△BCD的面积和使问题得到解决(如图2).
请回答:(1)△ABD的面积为 (用含m的式子表示).
(2)求四边形ABCD的面积.


|
|
 参考小凯思考问题的方法,解决问题:
参考小凯思考问题的方法,解决问题:
如图3,在四边形ABCD中,对角线AC、BD相交于
点O,
|
 (0°<
(0°< <90°),则四边形
<90°),则四边形 ABCD的面积为 (用含a、b、 的式子表示).
的式子表示).
解:(1) ;……………………………………………………………………………1分
;……………………………………………………………………………1分
 (2)由题意可知∠AEO=90°.
(2)由题意可知∠AEO=90°.
∵ AO= m ,∠AOB=30°,
∴AE= .
.
∴S△ABD= .
.
同理,CF= .
.
∴S△BCD= .…………………………………………………2分
.…………………………………………………2分
∴S四边形ABCD= S△ABD+S△BCD .…………………………………………………3分
.…………………………………………………3分
解决问题: .………………………………………………………………5分
.………………………………………………………………5分

练习册系列答案
相关题目
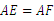 ;
; 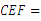 ∠
∠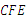 ;
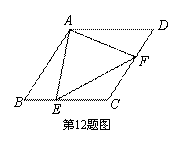
; 
 ,
,  AC长为半径画弧,两弧交点分别为点E、F,直线EF与AD相交于点O,若OA=2,则△ABC外接圆的面积为 .
AC长为半径画弧,两弧交点分别为点E、F,直线EF与AD相交于点O,若OA=2,则△ABC外接圆的面积为 .

 的图象与反比例函数
的图象与反比例函数
 的图象交于A (-3,1),B (1,n)两点.
的图象交于A (-3,1),B (1,n)两点. 接写出点
接写出点 的坐标.
的坐标.
 B.
B.
 D.
D.

 )个单位,得到矩形
)个单位,得到矩形 及其内部的点(
及其内部的点( .
. 的坐标为 ;
的坐标为 ; (1,4),
(1,4), (6,-4),求点
(6,-4),求点
