题目内容
如图,在△ABC中,CD是AB边上的中线,
已知∠B=45º,tan∠ACB=3,AC= ,
,
求:(1)△ABC的面积;(2)sin∠ACD的值.
(1)作AH⊥BC于H………………………………………………………(1分)
在Rt△ACH中,tan∠ACB=3,AC= ,∴CH=1,AH=3……………………(2分)
,∴CH=1,AH=3……………………(2分)
在Rt△ABH中,∠B=45°,∴BH=AH=3…………………………………………(3分)
 ∴S△ABC=
∴S△ABC=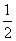 ×4×3=6…………………………………………………………………(4分)
×4×3=6…………………………………………………………………(4分)
 (2)作DE⊥AC于E,DF⊥BC于F
(2)作DE⊥AC于E,DF⊥BC于F
S△ACD=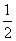 ×
× ×DE=3,∴
×DE=3,∴ DE=
DE=
 ……………………(5分)
……………………(5分)
在Rt△CDF中,CD= =
= ……………………(6分)
……………………(6分)
∴在Rt△CDE中,sin∠ACD= =
= …………………(8分)
…………………(8分)

 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案如图,点M、N分别在矩形ABCD边AD、BC上,将
 矩形ABCD沿MN翻折后点C恰好与点A重合,若
矩形ABCD沿MN翻折后点C恰好与点A重合,若
此时 =
= ,则△AMD′ 的面积与△AMN的面积的比为
,则△AMD′ 的面积与△AMN的面积的比为
A.1:3 B.1:4
C.1:6 D.1: 9
阅读下面材料:
小凯遇到这样一个问题:如图1,在四边形ABCD中,对角线AC、BD相交于点O,
AC=4,BD=6,∠AOB=30°,求四边形ABCD的面积.
小凯发现,分别过点A、C作直线BD的垂线,垂足分别为点E、F,设AO为m,通过计算△ABD与△BCD的面积和使问题得到解决(如图2).
请回答:(1)△ABD的面积为 (用含m的式子表示).
(2)求四边形ABCD的面积.


|
|
 参考小凯思考问题的方法,解决问题:
参考小凯思考问题的方法,解决问题:
如图3,在四边形ABCD中,对角线AC、BD相交于
点O,
|
 (0°<
(0°< <90°),则四边形
<90°),则四边形 ABCD的面积为 (用含a、b、 的式子表示).
的式子表示).
 ,则平均每次降价的百分率
,则平均每次降价的百分率 B.
B. C.
C. D.
D. 
 ,求AB的长.
,求AB的长.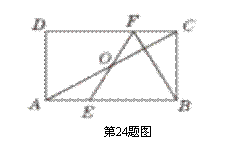


 合并的是
合并的是 B.
B. C.
C. D.
D.
