Question

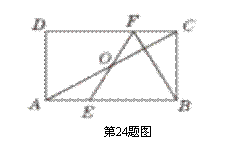
如图，在菱形ABCD中，∠B＝60°，点E，F分别从点B，D同时以同样的速度沿边BC，DC向点C运动.给出以下四个结论：

① ;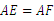

② ∠∠;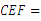

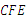③ 当点E，F分别为边BC，DC的中点时，△AEF是等边三角形；

④ 当点E，F分别为边BC，DC的中点时，△AEF的面积最大.

上述正确结论的序号有 .

Answer 1

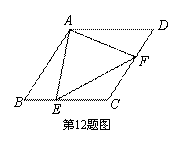
①②③  解析：因为四边形ABCD为菱形，所以ABCD，∠B=∠D，BE=DF，所以△≌△，所以AEAF，①正确.

由CB=CD，BE=DF,得CE=CF，所以∠CEF=∠CFE，②正确.

当E，F分别为BC，CD的中点时，BE=DF=BC=DC.连接AC，BD，知△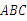为等边三角形，所以⊥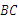.因为AC⊥BD,所以∠ACE=60°，∠CEF=30°，⊥，所以  ∠AEF=.由①知AEAF，故△为等边三角形，③正确.

设菱形的边长为1，当点E，F分别为边BC，DC的中点时，的面积为，而当点E，F分别与点B，D重合时，=，故④错.