Question

18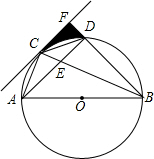．如图，在⊙O中，AB是直径，C是$\widehat{AD}$的中点，弦AD与BC交于点E，过点C的直线CF交BD的延长线于点F，且∠FCD=CBD．
（1）求证：CF是⊙O的切线；
（2）若AB=4，∠ABC=30°，求阴影部分的面积．

Answer 1

分析 （1）根据垂径定理可知OC⊥AD，只要证明CF∥AD即可证明CF⊥OC，由此解决问题．
（2）先证明△AOC、△COD都是等边三角形，再根据S_阴=S_△CDF-（S_扇形COD-S_△COD）计算即可．

解答 （1）证明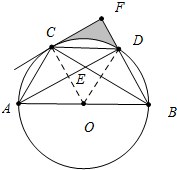：如图，连接OC．
∵C是$\widehat{AD}$的中点，
∴OC⊥AD，
∵∠FCD=CBD，∠CBD=∠ADC，
∴∠FCD=∠CDA，
∴CF∥AD，
∴CF⊥OC，
∴CF是⊙O切线．
（2）解：∵AB=4，∠ABC=30°，AB是直径，
∴∠ACB=90°，
∴∠CAB=60°，
∵$\widehat{AC}$=$\widehat{CD}$，OA=OC，
∴△AOC是等边三角形，
∴∠AOC=∠COD=60°=∠DOB，
∴△COD是等边三角形，
∴AC=CD=BD=2，
∵CF∥AD，
∴∠F=∠ADB=90°，
在RT△CDF中，∠FCD=30°，CD=2，
∴DF=$\frac{1}{2}$CD=1，CF=$\sqrt{C{D}^{2}-D{F}^{2}}$=$\sqrt{3}$，
∴S_阴=S_△CDF-（S_扇形COD-S_△COD）=$\frac{3\sqrt{3}}{2}$-$\frac{2π}{3}$．

点评 本题考查切线的判定、垂径定理、扇形的面积等知识，解题的关键是灵活运用圆的有关知识，学会利用分割法求阴影部分面积，属于中考常考题型．