题目内容
13.解下列不等式组:(1)$\left\{\begin{array}{l}{\frac{x-3}{2}+3≥x}\\{1-3(x-1)<8-x}\end{array}\right.$;
(2)$\left\{\begin{array}{l}{2x+4≤5(x+2)}\\{x-1<\frac{2}{3}x}\end{array}\right.$.
分析 (1)分别解出两不等式的解集再求其公共解.
(2)分别解出两不等式的解集再求其公共解.
解答 解:(1)$\left\{\begin{array}{l}{\frac{x-3}{2}+3≥x①}\\{1-3(x-1)<8-x②}\end{array}\right.$
由①得:x≤3;
由②得:x>-2;
故原不等式组的解集是:-2<x≤3.
(2)$\left\{\begin{array}{l}{2x+4≤5(x+2)①}\\{x-1<\frac{2}{3}x②}\end{array}\right.$
由①得:x≥-2;
由②得:x<3;
故原不等式组的解集是:-2≤x<3.
点评 本题考查了解一元一次不等式组,应遵循以下原则:同大取较大,同小取较小,小大大小中间找,大大小小解不了.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
3.下列运算正确的是( )
| A. | x+x=x2 | B. | x6÷x2=x3 | C. | (2x2)3=6x5 | D. | x•x3=x4 |
2.计算$\frac{{m}^{2}}{m-3}$-$\frac{9}{m-3}$的结果是( )
| A. | m+3 | B. | m-3 | C. | 3-m | D. | -m-3 |
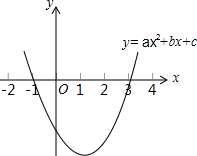 二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列说法:
二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列说法: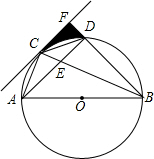 如图,在⊙O中,AB是直径,C是$\widehat{AD}$的中点,弦AD与BC交于点E,过点C的直线CF交BD的延长线于点F,且∠FCD=CBD.
如图,在⊙O中,AB是直径,C是$\widehat{AD}$的中点,弦AD与BC交于点E,过点C的直线CF交BD的延长线于点F,且∠FCD=CBD. 如图,在△ABC中,AB>AC,内切圆⊙I与边BC切于点D,AD与⊙I的另一个交点为E,⊙I的切线EP与BC的延长线交于点P,CF∥PE且与AD交于点F,直线BF与⊙I交于点M、N,M在线段BF上,线段PM与⊙I交于另一点Q.证明:∠ENP=∠ENQ.
如图,在△ABC中,AB>AC,内切圆⊙I与边BC切于点D,AD与⊙I的另一个交点为E,⊙I的切线EP与BC的延长线交于点P,CF∥PE且与AD交于点F,直线BF与⊙I交于点M、N,M在线段BF上,线段PM与⊙I交于另一点Q.证明:∠ENP=∠ENQ.