题目内容
 已知在平面直角坐标系中,点O为坐标原点,直线y=
已知在平面直角坐标系中,点O为坐标原点,直线y=| 3 |
| 4 |
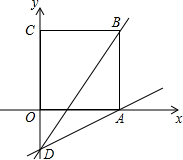
(1)求点B的坐标;
(2)点P(0,t)在线段OC(点p不与O、C点重合)上运动,过点P作PE∥DB交BC于点E,设线段BE的长为d,求d与t的函数关系式,并直接写出自变量t的取值范围;
(3)在(2)的条件下,点H为线段OC上一点,连接AP与直线DB交于点M,连接PB,当以PB为直径的圆经过点M时,恰好使∠MHO=∠OAD,求此时的t值及H点的坐标.
考点:一次函数综合题
专题:
分析:(1)根据直线y=
x-3求得A、D的坐标,把A的横坐标代入直线BD的解析式即可求得B的坐标;
(2)根据题意得出
=
,即
=
,即可求得d与t的函数关系式;
(3)根据题意设出直线AP的解析式为y=-
x+t,代入A的坐标即可求得t的值,根据直线AP和直线BD的解析式,求得交点M的坐标,然后根据△DOA∽△MNH,得出
=
,求得NH的长,即可求得H的坐标.
| 3 |
| 4 |
(2)根据题意得出
| CP |
| CD |
| CE |
| CB |
| 5-t |
| 8 |
| 4-d |
| 4 |
(3)根据题意设出直线AP的解析式为y=-
| 1 |
| 2 |
| HN |
| OA |
| MN |
| OD |
解答:解:(1)∵直线y=
x-3,
∴A(4,0),D(0,-3),
∵直线y=2x+b经过点D,
∴b=-3,
∴直线BD为:y=2x-3,
∵AB⊥x轴,
把x=4代入得,y=2×4-3=5,
∴点B的坐标为(4,5);
(2)如图①,∵B(4,5),BC⊥y轴于点C,
∴C(0,5),
∴CD=8,BC=4,
∵PE∥DB,
∴
=
,即
=
,
∴d=
t+
(0<t<5);
(3)如图②,∵以PB为直径的圆经过点M,
∴∠PMB=90°,
∵直线BD为:y=2x-3,
∴设直线AP的解析式为y=-
x+t,
∵A((4,0),
代入得0=-
×4+t,解得t=2,
∴直线AP的解析式为y=-
x+2,
解
,得
,
∴M(2,1),
作MN⊥y轴于N,则MN=2.
∵∠AOD=∠MNH=90°,∠MHO=∠OAD,
∴△DOA∽△MNH,
∴
=
,即
=
,解得NH=
,
∴OH=
+1=
,
∴H(0,
).
| 3 |
| 4 |
∴A(4,0),D(0,-3),
∵直线y=2x+b经过点D,
∴b=-3,
∴直线BD为:y=2x-3,
∵AB⊥x轴,
把x=4代入得,y=2×4-3=5,

∴点B的坐标为(4,5);
(2)如图①,∵B(4,5),BC⊥y轴于点C,
∴C(0,5),
∴CD=8,BC=4,
∵PE∥DB,
∴
| CP |
| CD |
| CE |
| CB |
| 5-t |
| 8 |
| 4-d |
| 4 |
∴d=
| 1 |
| 2 |
| 3 |
| 2 |
(3)如图②,∵以PB为直径的圆经过点M,

∴∠PMB=90°,
∵直线BD为:y=2x-3,
∴设直线AP的解析式为y=-
| 1 |
| 2 |
∵A((4,0),
代入得0=-
| 1 |
| 2 |
∴直线AP的解析式为y=-
| 1 |
| 2 |
解
|
|
∴M(2,1),
作MN⊥y轴于N,则MN=2.
∵∠AOD=∠MNH=90°,∠MHO=∠OAD,
∴△DOA∽△MNH,
∴
| HN |
| OA |
| MN |
| OD |
| NH |
| 4 |
| 2 |
| 3 |
| 8 |
| 3 |
∴OH=
| 8 |
| 3 |
| 11 |
| 3 |
∴H(0,
| 11 |
| 3 |
点评:本题是一次函数的综合题,考查了待定系数法求解析式,点的坐标特征,平行线分线段成比例定理,直线的交点的求法三角形相似的判定和性质等.

练习册系列答案
相关题目
 已知点A在⊙O上,根据sinB=
已知点A在⊙O上,根据sinB=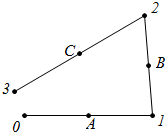 如图,平面内有不在同一直线上的三个定点A,B,C,一只青蛙从图中的0号位置出发,跳到关于点A对称的1号位置,再跳到关于点B对称的2号位置,然后又跳到关于点C对称的3号位置,在跳到关于A对称的4号位置,如此继续,一直对称的跳下去,现在要问:第2004号位置与0号位置之间的距离是多少?
如图,平面内有不在同一直线上的三个定点A,B,C,一只青蛙从图中的0号位置出发,跳到关于点A对称的1号位置,再跳到关于点B对称的2号位置,然后又跳到关于点C对称的3号位置,在跳到关于A对称的4号位置,如此继续,一直对称的跳下去,现在要问:第2004号位置与0号位置之间的距离是多少?