题目内容
17.计算:$\sqrt{27}$-(-1)2016-3tan60°+(-2016)0化简:$\frac{1}{a+1}$-$\frac{a}{{(a+1)}^{2}}$.
分析 原式利用二次根式性质,乘方的意义,零指数幂法则,以及特殊角的三角函数值计算即可得到结果;
原式通分并利用同分母分式的减法法则计算即可得到结果.
解答 解:原式=3$\sqrt{3}$-1-3$\sqrt{3}$+1=0;
原式=$\frac{a+1}{(a+1)^{2}}$-$\frac{a}{(a+1)^{2}}$=$\frac{1}{{{{({a+1})}^2}}}$.
点评 此题考查了分式的加减法,以及实数的运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
8.学校要举行“诗词大会”,七、八年级每班选拔一人参加最终的决赛.七年级一班通过层层选拔,最后要从A同学和B同学中选择一人参加学校的比赛,语文老师给这两位同学进行了10次诗词相关知识的测试,计分采用10分制(得分均取整数),成绩达到6分或6分以上为及格,达到9分或10分为优秀.成绩如表1所示,并制作了成绩分析表(表2)
表1
表2
(1)在表2中,a=8,b=8,c=10,d=2.8,e=90%,f=30%;
(2)有人说B同学成绩比A同学成绩好;但也有人坚定认为A同学成绩比B同学成绩好.请你分别给出支持A同学或支持B同学的理由.
表1
| A同学 | 5 | 8 | 8 | 9 | 8 | 10 | 9 | 8 | 8 | 5 |
| B同学 | 10 | 7 | 7 | 9 | 10 | 5 | 8 | 6 | 10 | 8 |
| 同学 | 平均分 | 中位数 | 众数 | 方差 | 及格率 | 优秀率 |
| A | 7.8 | b | 8 | 2.36 | 80% | f |
| B | a | 7 | c | d | e | 40% |
(2)有人说B同学成绩比A同学成绩好;但也有人坚定认为A同学成绩比B同学成绩好.请你分别给出支持A同学或支持B同学的理由.
6.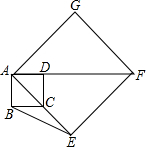 如图,正方形ABCD的顶点C在正方形AEFG的边AE上,AB=2,AE=4$\sqrt{2}$,则点G到BE的距离( )
如图,正方形ABCD的顶点C在正方形AEFG的边AE上,AB=2,AE=4$\sqrt{2}$,则点G到BE的距离( )
 如图,正方形ABCD的顶点C在正方形AEFG的边AE上,AB=2,AE=4$\sqrt{2}$,则点G到BE的距离( )
如图,正方形ABCD的顶点C在正方形AEFG的边AE上,AB=2,AE=4$\sqrt{2}$,则点G到BE的距离( )| A. | $\frac{32\sqrt{2}}{5}$ | B. | $\frac{36\sqrt{2}}{5}$ | C. | $\frac{16\sqrt{5}}{5}$ | D. | $\frac{18\sqrt{5}}{5}$ |
7.如图1,在等边△ABC中,动点P从点A出发,沿三角形的边由A→C→B作匀速运动,设点P运动的路程为x,△ABP的面积为y,把y看作x的函数,函数的图象如图2所示,则△ABC的面积为( )


| A. | 4$\sqrt{3}$ | B. | 8$\sqrt{3}$ | C. | 8 | D. | 16 |
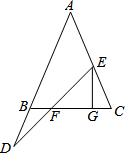 如图,∠ABC=∠C,点E在线段AC上,D在AB的延长线上,且有BD=CE,连接DE交BC于F,过E作FG⊥BC于G.试说明线段EF、FG、CG之间的数量关系.
如图,∠ABC=∠C,点E在线段AC上,D在AB的延长线上,且有BD=CE,连接DE交BC于F,过E作FG⊥BC于G.试说明线段EF、FG、CG之间的数量关系.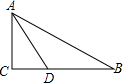 如图,在Rt△ABC中,∠C=90°,AD平分∠BAC交BC于点D,若∠B=30°,BD=6,则CD的长为3.
如图,在Rt△ABC中,∠C=90°,AD平分∠BAC交BC于点D,若∠B=30°,BD=6,则CD的长为3.
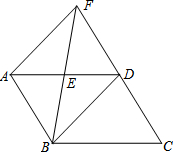 如图,在□ABCD中,E是AD边上的中点,连接BE,并延长BE交CD的延长线于点F,连接BD、AF,BE平分∠ABD,∠ABD=60°.
如图,在□ABCD中,E是AD边上的中点,连接BE,并延长BE交CD的延长线于点F,连接BD、AF,BE平分∠ABD,∠ABD=60°.