Question

2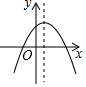．已知二次函数y=ax²+bx+c的图象如图，在同一直角坐标系中，一次函数y=cx+a和反比例函数y=$\frac{b}{x}$的图象大致是（　　）

• A．
• B．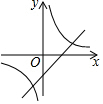
• C．
• D．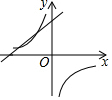

Answer 1

分析 根据二次函数图象开口方向与对称轴判断出a、b的正负情况，再根据二次函数图象与y轴的交点判断出c的正负情况，然后根据一次函数图象与系数的关系，反比例函数图象与系数的关系判断出两图象的大致情况即可得解．

解答 解：∵二次函数图象开口向下，
∴a＜0，
∵对称轴x=-$\frac{b}{2a}$＞0，
∴b＞0，
∵二次函数图象与y轴交于正半轴，
∴c＞0，
∴一次函数y=cx+a过第一三四象限，反比例函数y=$\frac{b}{x}$位于第一三象限，
纵观各选项，只有B选项符合．
故选：B．

点评 本题考查了二次函数图象，一次函数图象，反比例函数图象，根据二次函数图象判断出a、b、c的情况是解题的关键，也是本题的难点．