题目内容
15. 如图,AB⊥BD于点B,CD⊥BD于点D,∠1+∠2=180°,试说明:CD∥EF
如图,AB⊥BD于点B,CD⊥BD于点D,∠1+∠2=180°,试说明:CD∥EF解:∵AB⊥BD
∴∠B=90°垂直的定义
又∵CD⊥BD
∴∠D=90°
∴∠B+∠D=180°
∴AB∥CD
又∠1+∠2=180° (已知)
∴AB∥EF
∴CD∥EF平行公理的推论.
分析 根据垂直的定义得到∠B=90°,∠D=90°,得到∠B+∠D=180°,推出AB∥CD,AB∥EF于是得到结论.
解答 解:∵AB⊥BD,
∴∠B=90°(垂直的定义),
又∵CD⊥BD,
∴∠D=90°,
∴∠B+∠D=180°,
∴AB∥CD,
又∠1+∠2=180° (已知)
∴AB∥EF
∴CD∥EF(平行公理的推论).
故答案为:垂直的定义,BD,90°,180°,AB,CD,AB,EF,平行公理的推论.
点评 本题考查了平行线的判定和性质,垂直的定义,熟练掌握平行线的判定和性质是解题的关键.

练习册系列答案
 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案
相关题目
6.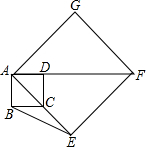 如图,正方形ABCD的顶点C在正方形AEFG的边AE上,AB=2,AE=4$\sqrt{2}$,则点G到BE的距离( )
如图,正方形ABCD的顶点C在正方形AEFG的边AE上,AB=2,AE=4$\sqrt{2}$,则点G到BE的距离( )
 如图,正方形ABCD的顶点C在正方形AEFG的边AE上,AB=2,AE=4$\sqrt{2}$,则点G到BE的距离( )
如图,正方形ABCD的顶点C在正方形AEFG的边AE上,AB=2,AE=4$\sqrt{2}$,则点G到BE的距离( )| A. | $\frac{32\sqrt{2}}{5}$ | B. | $\frac{36\sqrt{2}}{5}$ | C. | $\frac{16\sqrt{5}}{5}$ | D. | $\frac{18\sqrt{5}}{5}$ |
3.在a3•a2•( )=a12中,括号内应填写的代数式是( )
| A. | a7 | B. | a6 | C. | a8 | D. | a3 |
7.如图1,在等边△ABC中,动点P从点A出发,沿三角形的边由A→C→B作匀速运动,设点P运动的路程为x,△ABP的面积为y,把y看作x的函数,函数的图象如图2所示,则△ABC的面积为( )


| A. | 4$\sqrt{3}$ | B. | 8$\sqrt{3}$ | C. | 8 | D. | 16 |
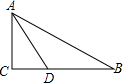 如图,在Rt△ABC中,∠C=90°,AD平分∠BAC交BC于点D,若∠B=30°,BD=6,则CD的长为3.
如图,在Rt△ABC中,∠C=90°,AD平分∠BAC交BC于点D,若∠B=30°,BD=6,则CD的长为3. 若画图并填空:
若画图并填空: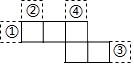 由五个全等正方形组成的图形如图所示,将一个同样大小的正方形放在图中的①、②、③、④某一位置,所组成的图形不是正方体表面展开图的是( )
由五个全等正方形组成的图形如图所示,将一个同样大小的正方形放在图中的①、②、③、④某一位置,所组成的图形不是正方体表面展开图的是( ) 如图,在正方形ABCD中,有一个面积为25的小正方形EFGH,其中E、F、G、H分别在AB、BC、FD上,若BF=4,则AB的长为( )
如图,在正方形ABCD中,有一个面积为25的小正方形EFGH,其中E、F、G、H分别在AB、BC、FD上,若BF=4,则AB的长为( )