题目内容
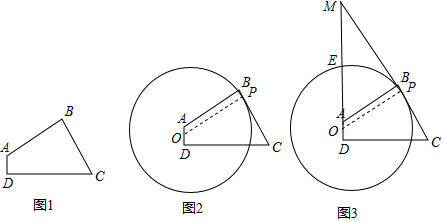
16.如图1,四边形ABCD是一条河入海口的一部分,AB,CD是河的两岸,AD是河上原有的古桥,由于交通的发展,古桥的通行能边远远不能满足人们出行的需要,为了保护古桥AD,重新规划建一座新桥BC;已知,古桥AD与河岸CD垂直,新桥BC与河岸AB垂直,且BC=AB,CD=210m,tan∠BCD=$\frac{4}{3}$.(1)分别求古桥DA与新桥BC的长;
(2)因为古桥周边的古建筑比较多,为了保护古建筑,根据规划,建新桥的同时,将对古桥周边设立一个圆形保护区(如图2),圆心O在线段AD上,圆形保护区的边界与BC相切;设保护区半径为R,DO=xm.试求半径R与x的关系式;
(3)如图3,点M是线段CB与DA延长线的交点,若点M到保护区边缘最小距离为110m,求此时的O,D两点间的距离.
分析 (1)点M是线段CB与DA延长线的交点,如图1,先在Rt△CDM中利用正切定义计算出MD=280,再利用勾股定理计算出MC=350,接着证明∠MAB=∠C,由于tan∠MAB=$\frac{BM}{AB}$=$\frac{4}{3}$,于是可设MB=4x,则AB=3x,MA=5x,然后利用MC的长可求出x=50,最后计算BC、MA和AD的长;
(2)点M是线段CB与DA延长线的交点,如图2,利用切线的性质得OP⊥BC,则OP∥AB,于是可证明△MAB∽△MOP,利用相似比得250:(280-x)=150:R,从而得到R与x的关系式;
(3)如图3,⊙P与MD相交于点E,利用ME=110得到DE=170,则R+x=170,然后把(2)中的关系式代入可求出x的值.
解答 解:(1)点M是线段CB与DA延长线的交点,如图1,
∵AD⊥CD,CB⊥AB,
∴∠D=∠ABC=90°,
在Rt△CDM中,∵tanC=$\frac{MD}{CD}$=$\frac{4}{3}$,
∴MD=$\frac{4}{3}$×210=280,
∴MC=$\sqrt{21{0}^{2}+28{0}^{2}}$=350,
∵∠M+∠C=90°,∠M+∠MAB=90°,
∴∠MAB=∠C,
在Rt△MAB中,tan∠MAB=$\frac{BM}{AB}$=$\frac{4}{3}$,
设MB=4x,AB=3x,则MA=$\sqrt{(3x)^{2}+(4x)^{2}}$=5x,
∵BC=AB=3x,
∴4x+3x=350,解得x=50,
∴BC=3x=150, MA=5x=250,
MA=5x=250,
AD=MD-MA=280-250=30,
答:古桥DA为30m,新桥BC的长为150m;
(2)点M是线段CB与DA延长线的交点,如图2,
∵⊙O与BC相切于点P,
∴OP⊥BC,
∴OP∥AB,
∴△MAB∽△MOP,
∴MA:MO=AB:OP,
即250:(280-x)=150:R,
∴R=-$\frac{3}{5}$x+168(0≤x≤3);
(3)如图3,⊙P与MD相交于点E,
∵点M到⊙P的最小距离为110,
∴ME=110,
∴DE=280-110=170,
∵OE+OD=DE,
∴R+x=170,
而R=-$\frac{3}{5}$x+168,
∴-$\frac{3}{5}$x+168+x=170,解得x=5,
即此时的O,D两点间的距离为5m.
点评 本题考查了圆的综合题:熟练掌握切线的性质和相似三角形的判定与性质;能构建直角三角形,会利用锐角三角函数的定义、勾股定理和相似比进行几何计算.

 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案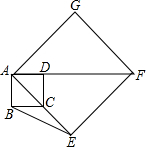 如图,正方形ABCD的顶点C在正方形AEFG的边AE上,AB=2,AE=4$\sqrt{2}$,则点G到BE的距离( )
如图,正方形ABCD的顶点C在正方形AEFG的边AE上,AB=2,AE=4$\sqrt{2}$,则点G到BE的距离( )| A. | $\frac{32\sqrt{2}}{5}$ | B. | $\frac{36\sqrt{2}}{5}$ | C. | $\frac{16\sqrt{5}}{5}$ | D. | $\frac{18\sqrt{5}}{5}$ |

| A. | 4$\sqrt{3}$ | B. | 8$\sqrt{3}$ | C. | 8 | D. | 16 |
| A. | -402 | B. | $\frac{5}{9}$ | C. | $\frac{9}{5}$ | D. | $\frac{670}{3}$ |
 如图,在正方形ABCD中,有一个面积为25的小正方形EFGH,其中E、F、G、H分别在AB、BC、FD上,若BF=4,则AB的长为( )
如图,在正方形ABCD中,有一个面积为25的小正方形EFGH,其中E、F、G、H分别在AB、BC、FD上,若BF=4,则AB的长为( )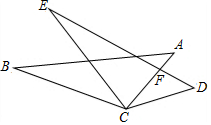 如图,CA=CD,AB=DE,BC=EC,AC与DE相交于点F,若∠EFC=75°,∠D=40°,则∠BCE=35°.
如图,CA=CD,AB=DE,BC=EC,AC与DE相交于点F,若∠EFC=75°,∠D=40°,则∠BCE=35°.