题目内容
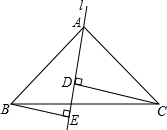 已知,如图,△ABC中,∠BAC=90°,AB=AC,l是过A的一条直线,BE⊥l于E,
已知,如图,△ABC中,∠BAC=90°,AB=AC,l是过A的一条直线,BE⊥l于E,CD⊥l于D.
(1)求证:BE=AD;
(2)若BE=5,CD=7,求DE的长.
考点:全等三角形的判定与性质,等腰直角三角形
专题:
分析:(1)先根据∠BAC=90°得出∠BAE+∠CAD=90°,再根据BE⊥AE可知∠BAE+∠ABE=90°,故可得出∠CAD=∠ABE,根据AAS定理可得出△ABE≌△CAD,由此得出结论;
(2)根据(1)中△ABE≌△CAD可得出AE及AD的长,进而得出结论.
(2)根据(1)中△ABE≌△CAD可得出AE及AD的长,进而得出结论.
解答:(1)证明:∵∠BAC=90°,
∴∠BAE+∠CAD=90°.
∵BE⊥AE,
∴∠BAE+∠ABE=90°,
∴∠CAD=∠ABE,
在△ABE与△CAD中,
,
∴△ABE≌△CAD(AAS).
∴BE=AD;
(2)解:∵由(1)知△ABE≌△CAD,
∴BE=AD=5,AE=CD=7,
∴DE=AE-AD=7-5=2.
∴∠BAE+∠CAD=90°.
∵BE⊥AE,
∴∠BAE+∠ABE=90°,
∴∠CAD=∠ABE,
在△ABE与△CAD中,
|
∴△ABE≌△CAD(AAS).
∴BE=AD;
(2)解:∵由(1)知△ABE≌△CAD,
∴BE=AD=5,AE=CD=7,
∴DE=AE-AD=7-5=2.
点评:本题考查的是全等三角形的判定定理,熟知AAS、ASA、SAS、SSS定理是解答此题的关键.

练习册系列答案
相关题目
下列各式:
,
(b≥2),
,
,
,其中是二次根式的个数有( )
| a2+1 |
| b+2 |
| -(3x-1)2 |
(-
|
| b2-4ac |
| A、2个 | B、3个 | C、4个 | D、5个 |
 如图,已知一次函数y=ax-2的图象与反比例函数y=
如图,已知一次函数y=ax-2的图象与反比例函数y= 作图题:(不要求写作法)
作图题:(不要求写作法) 如图,在Rt△ABC中,∠BAC=90°,D为BC的中点,连接AD,E为AB上一点,过E作EF∥BC交AD于F.
如图,在Rt△ABC中,∠BAC=90°,D为BC的中点,连接AD,E为AB上一点,过E作EF∥BC交AD于F. 如图,M、N是正方形ABCD边AB、CD上两动点,连接MN,将四边形BCNM沿MN折叠,使点B落在AD边上点E处、点C落在点F.
如图,M、N是正方形ABCD边AB、CD上两动点,连接MN,将四边形BCNM沿MN折叠,使点B落在AD边上点E处、点C落在点F. 如图,矩形ABCD中,AB=2,BC=3,以点A为圆心AB为半径画弧交AD于E,以点C为圆心、CB为半径画弧交CD延长线于F,则图中阴影部分面积为
如图,矩形ABCD中,AB=2,BC=3,以点A为圆心AB为半径画弧交AD于E,以点C为圆心、CB为半径画弧交CD延长线于F,则图中阴影部分面积为