题目内容
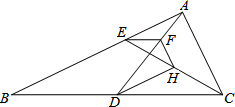 如图,在Rt△ABC中,∠BAC=90°,D为BC的中点,连接AD,E为AB上一点,过E作EF∥BC交AD于F.
如图,在Rt△ABC中,∠BAC=90°,D为BC的中点,连接AD,E为AB上一点,过E作EF∥BC交AD于F.(1)求证:EF=AF.
(2)若H为EC的中点,连接FH、DH,求证:DH⊥FH.
考点:全等三角形的判定与性质,直角三角形斜边上的中线
专题:证明题
分析:(1)根据直角三角形斜边上的中线等于斜边的一半可得AD=BD=CD,再根据等边对等角可得∠B=∠BAD,根据两直线平行,同位角相等可得∠B=∠AEF,从而得到∠AEF=∠BAD,再根据等角对等边可得EF=AF;
(2)延长FH交BC于G,根据线段中点的定义可得EH=CH,两直线平行,内错角相等可得∠FEH=∠GCH,然后利用“角边角”证明△EFH和△CGH全等,根据全等三角形对应边相等可得FH=GH,EF=CG,再求出DF=DG,然后根据等腰三角形三线合一的证明即可.
(2)延长FH交BC于G,根据线段中点的定义可得EH=CH,两直线平行,内错角相等可得∠FEH=∠GCH,然后利用“角边角”证明△EFH和△CGH全等,根据全等三角形对应边相等可得FH=GH,EF=CG,再求出DF=DG,然后根据等腰三角形三线合一的证明即可.
解答:证明:(1)∵∠BAC=90°,D为BC的中点,
∴AD=BD=CD,
∴∠B=∠BAD,
∵EF∥BC,
∴∠B=∠AEF,
∴∠AEF=∠BAD,
∴EF=AF;
(2)如图,延长FH交BC于G,
∵H为EC的中点,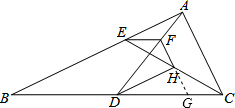
∴EH=CH,
∵EF∥BC,
∴∠FEH=∠GCH,
在△EFH和△CGH中,
,
∴△EFH≌△CGH(ASA),
∴FH=GH,EF=CG,
∵EF=AF=CG,AD=CD,
∴AD-AF=CD-CG,
即DF=DG,
又∵DF=DG,FH=GH,
∴DH⊥FH.
∴AD=BD=CD,
∴∠B=∠BAD,
∵EF∥BC,
∴∠B=∠AEF,
∴∠AEF=∠BAD,
∴EF=AF;
(2)如图,延长FH交BC于G,
∵H为EC的中点,

∴EH=CH,
∵EF∥BC,
∴∠FEH=∠GCH,
在△EFH和△CGH中,
|
∴△EFH≌△CGH(ASA),
∴FH=GH,EF=CG,
∵EF=AF=CG,AD=CD,
∴AD-AF=CD-CG,
即DF=DG,
又∵DF=DG,FH=GH,
∴DH⊥FH.
点评:本题考查了全等三角形的判定与性质,等腰三角形三线合一的性质,直角三角形斜边上的中线等于斜边的一半的性质,熟记各性质是解题的关键,(2)难点在于作辅助线构造出全等三角形和等腰三角形.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
有下列各数
,10,3.14,-
,0,-(-3),-|-5|,-(-42),其中属于非负整数的共有( )
| 1 |
| 2 |
| 2 |
| 3 |
| A、3个 | B、4个 | C、5个 | D、6个 |
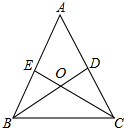 已知:如图,锐角△ABC的两条高BD,CE相交于点O,且OB=OC.
已知:如图,锐角△ABC的两条高BD,CE相交于点O,且OB=OC.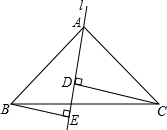 已知,如图,△ABC中,∠BAC=90°,AB=AC,l是过A的一条直线,BE⊥l于E,
已知,如图,△ABC中,∠BAC=90°,AB=AC,l是过A的一条直线,BE⊥l于E,