题目内容
 如图,矩形ABCD中,AB=2,BC=3,以点A为圆心AB为半径画弧交AD于E,以点C为圆心、CB为半径画弧交CD延长线于F,则图中阴影部分面积为
如图,矩形ABCD中,AB=2,BC=3,以点A为圆心AB为半径画弧交AD于E,以点C为圆心、CB为半径画弧交CD延长线于F,则图中阴影部分面积为考点:扇形面积的计算
专题:
分析:根据扇形的面积公式即可求得扇形ABE的面积S1,扇形CBF的面积S2,根据矩形的面积公式求得矩形的面积S3,根据S阴影=S2-(S3-S1)即可求解.
解答:解:扇形ABE的面积S1=
=π,
扇形CBF的面积S2=
=
,
矩形ABCD的面积是:S3=AB•BC=2×3=6,
则S阴影=S2-(S3-S1)=
-(6-π)=
-6.
故答案是:
-6.
| 90π×22 |
| 360 |
扇形CBF的面积S2=
| 90π×32 |
| 360 |
| 9π |
| 4 |
矩形ABCD的面积是:S3=AB•BC=2×3=6,
则S阴影=S2-(S3-S1)=
| 9π |
| 4 |
| 13π |
| 4 |
故答案是:
| 13π |
| 4 |
点评:本题考查了扇形的面积公式,正确理解S阴影=S2-(S3-S1)是关键.

练习册系列答案
 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
下列计算正确的是( )
| A、a+2a=3a2 |
| B、(a5)2=a7 |
| C、a2×a3=a5 |
| D、a6÷a3=a2 |
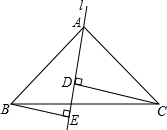 已知,如图,△ABC中,∠BAC=90°,AB=AC,l是过A的一条直线,BE⊥l于E,
已知,如图,△ABC中,∠BAC=90°,AB=AC,l是过A的一条直线,BE⊥l于E, 如图,已知AB=12米,MA⊥AB于A,MA=6米,射线BD⊥AB于B,P点从B向A运动,每秒走1米,Q点从B向D运动,每秒走2米,P、Q同时从B出发,则出发
如图,已知AB=12米,MA⊥AB于A,MA=6米,射线BD⊥AB于B,P点从B向A运动,每秒走1米,Q点从B向D运动,每秒走2米,P、Q同时从B出发,则出发 如图,△ABC中,∠A=35°,沿BE将此三角形对折,又沿BA′再一次对折,点C落在BE上的C′处,此时∠C′DB=85°,则原三角形的∠ABC的度数为
如图,△ABC中,∠A=35°,沿BE将此三角形对折,又沿BA′再一次对折,点C落在BE上的C′处,此时∠C′DB=85°,则原三角形的∠ABC的度数为