题目内容
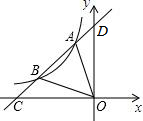如图，一次函数y=kx+4的图象与反比例函数y=| m |
| x |
考点：反比例函数与一次函数的交点问题
专题：
分析：先把y=kx+4代入y=
，整理得kx2+4x-m=0，解方程求出x的值，得到A（
，2+
），B（
，2-
）．再由一次函数y=kx+4的图象与x轴，y轴分别交于C、D两点，求出C（-
，0），D（0，4），然后根据两点之间的距离公式求出AC2=（
+
）2+（2+
-0）2=（
）2+（2+
）2，BD2=（
-0）2+（2-
-4）2=（
）2+（2+
）2，从而证明AC=BD．
| m |
| x |
-2+
| ||
| k |
| km+4 |
-2-
| ||
| k |
| km+4 |
| 4 |
| k |
-2+
| ||
| k |
| 4 |
| k |
| km+4 |
2+
| ||
| k |
| km+4 |
-2-
| ||
| k |
| km+4 |
2+
| ||
| k |
| km+4 |
解答：解：把y=kx+4代入y=
，得kx+4=
，
整理，得kx2+4x-m=0，
解得x=
，
所以A（
，2+
），B（
，2-
）．
∵一次函数y=kx+4的图象与x轴，y轴分别交于C、D两点，
∴C（-
，0），D（0，4）．
∵AC2=（
+
）2+（2+
-0）2=（
）2+（2+
）2，
BD2=（
-0）2+（2-
-4）2=（
）2+（2+
）2，
∴AC2=BD2，
∴AC=BD．
| m |
| x |
| m |
| x |
整理，得kx2+4x-m=0，
解得x=
-2±
| ||
| k |
所以A（
-2+
| ||
| k |
| km+4 |
-2-
| ||
| k |
| km+4 |
∵一次函数y=kx+4的图象与x轴，y轴分别交于C、D两点，
∴C（-
| 4 |
| k |
∵AC2=（
-2+
| ||
| k |
| 4 |
| k |
| km+4 |
2+
| ||
| k |
| km+4 |
BD2=（
-2-
| ||
| k |
| km+4 |
2+
| ||
| k |
| km+4 |
∴AC2=BD2，
∴AC=BD．
点评：本题考查了反比例函数与一次函数的交点问题，两点之间的距离公式，正确求出交点坐标是解题的关键．
练习册系列答案
相关题目
如图，已知直角梯形OABC的边OA在y轴的正半轴，OC在x轴的正半轴上，OA=AB=2，OC=3，D点是x轴正半轴的一动点，过点B作BE⊥BD交y轴的正半轴于点E．
如图，在△ABC中，DE∥BC，且分别交AB、AC于点D、E，BE、CD交于点O，证明：已知函数y=（m+2）x2-2x-1的图象与x轴有交点，则k的取值范围是（ ）
| A、m＞-3 |
| B、m≥-3 |
| C、m＞-3且m≠-2 |
| D、m≥-3且m≠-2 |
将一张正方形纸片沿一对角线对折后，得到一个等腰三角形，再沿底边上的高线对折，把得到的图形（如图）沿虚线剪开，打开阴影部分并铺开，此图形的对称轴有（ ）