题目内容
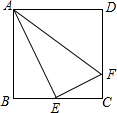 如图,在正方形ABCD中,E是BC的中点,F是CD上一点,且CF:CD=1:4,给出下列结论:①△ABE∽△ECF;②△ABE∽△AEF;③AE⊥EF;④△ADF∽△ECF.其中正确结论的序号为
如图,在正方形ABCD中,E是BC的中点,F是CD上一点,且CF:CD=1:4,给出下列结论:①△ABE∽△ECF;②△ABE∽△AEF;③AE⊥EF;④△ADF∽△ECF.其中正确结论的序号为考点:相似三角形的判定与性质
专题:
分析:容易证明①△ABE∽△ECF;利用①可得∠AEB+∠FEC=90°,可得③AE⊥EF;且可得
=2,且
=2,可证得②△ABE∽△AEF,而
≠
,所以④不正确.
| AE |
| EF |
| AB |
| BE |
| AD |
| CE |
| DF |
| CF |
解答:解:∵E为BC中点,CF:CD=1:4,
∴
=
=2,且∠B=∠C,
∴△ABE∽△ECF,
∴①正确;
∴∠BAE=∠FEC,且∠BAF+∠AFB=90°,
∴∠AFB+∠FEC=90°,
∴∠AEF=90°,
∴AE⊥EF,
∴③正确;
由①可得
=
=2,
∴
=
=
,且∠ABE=∠AEF=90°,
∴△ABE∽△AEF,
∴②正确;
∵
=2,
=3,
∴
≠
,
∴△ADF和△ECF不相似,
∴④不正确,
综上可知正确的为:①②③,
故答案为:①②③.
∴
| AB |
| CE |
| BE |
| CF |
∴△ABE∽△ECF,
∴①正确;
∴∠BAE=∠FEC,且∠BAF+∠AFB=90°,
∴∠AFB+∠FEC=90°,
∴∠AEF=90°,
∴AE⊥EF,
∴③正确;
由①可得
| AE |
| EF |
| AB |
| EC |
∴
| AB |
| AE |
| EC |
| EF |
| BE |
| EF |
∴△ABE∽△AEF,
∴②正确;
∵
| DA |
| CE |
| DF |
| CF |
∴
| AD |
| CE |
| DF |
| CF |
∴△ADF和△ECF不相似,
∴④不正确,
综上可知正确的为:①②③,
故答案为:①②③.
点评:本题主要考查相似三角形的判定和性质,掌握相似三角形的判定方法是解题的关键,注意正方形性质的运用.

练习册系列答案
 优加精卷系列答案
优加精卷系列答案
相关题目
已知函数y=(m+2)x2-2x-1的图象与x轴有交点,则k的取值范围是( )
| A、m>-3 |
| B、m≥-3 |
| C、m>-3且m≠-2 |
| D、m≥-3且m≠-2 |
下列各式从左到右的变形不正确的是( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
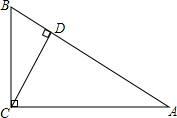 在Rt△ABC中,∠ACB=90°,AC=
在Rt△ABC中,∠ACB=90°,AC= 如图,在△ABC中,DE∥BC,且分别交AB、AC于点D、E,BE、CD交于点O,证明:
如图,在△ABC中,DE∥BC,且分别交AB、AC于点D、E,BE、CD交于点O,证明: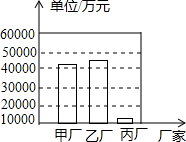 下表中列出了今年6月份三家牛奶生产厂家的利润额,所示的统计图:
下表中列出了今年6月份三家牛奶生产厂家的利润额,所示的统计图: