题目内容
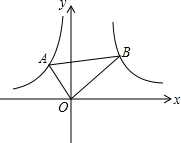 如图,在函数y=-
如图,在函数y=-| 1 |
| x |
| 4 |
| x |
| OA |
| OB |
考点:相似三角形的判定与性质,反比例函数图象上点的坐标特征
专题:
分析:分别过A和B作x轴的垂线,垂足分别为C、D,则由条件可证明△AOC∽△OBD,且利用反比例函数k的几何意义可得S△AOC=
,S△OBD=2,则可得出
.
| 1 |
| 2 |
| OA |
| OB |
解答: 解:如图,分别过A和B作x轴的垂线,垂足分别为C、D,
解:如图,分别过A和B作x轴的垂线,垂足分别为C、D,
则得S△AOC=
,S△OBD=2,
∵AO⊥OB,
∴∠CAO+∠AOC=∠AOC+∠BOD=90°,
∴∠CAO=∠BOD,
∴△AOC∽△OBD,
∴
=
=
=
,
故答案为:
.
 解:如图,分别过A和B作x轴的垂线,垂足分别为C、D,
解:如图,分别过A和B作x轴的垂线,垂足分别为C、D,则得S△AOC=
| 1 |
| 2 |
∵AO⊥OB,
∴∠CAO+∠AOC=∠AOC+∠BOD=90°,
∴∠CAO=∠BOD,
∴△AOC∽△OBD,
∴
| OA |
| OB |
|
|
| 1 |
| 2 |
故答案为:
| 1 |
| 2 |
点评:本题主要考查相似三角形的判定和性质,利用反比例函数y=
中k的几何意义求得S△AOC=
,S△OBD=2是解题的关键.
| k |
| x |
| 1 |
| 2 |

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知函数y=(m+2)x2-2x-1的图象与x轴有交点,则k的取值范围是( )
| A、m>-3 |
| B、m≥-3 |
| C、m>-3且m≠-2 |
| D、m≥-3且m≠-2 |
如果a=-a,那么表示a的点在数轴上的位置是( )
| A、原点的左边 | B、原点的右边 |
| C、原点 | D、无法确定 |
下列两个图形一定相似的是( )
| A、任意两个等腰三角形 |
| B、任意两个含30°角的直角三角形 |
| C、任意两个矩形 |
| D、任意两个菱形 |
 如图,已知直角梯形OABC的边OA在y轴的正半轴,OC在x轴的正半轴上,OA=AB=2,OC=3,D点是x轴正半轴的一动点,过点B作BE⊥BD交y轴的正半轴于点E.
如图,已知直角梯形OABC的边OA在y轴的正半轴,OC在x轴的正半轴上,OA=AB=2,OC=3,D点是x轴正半轴的一动点,过点B作BE⊥BD交y轴的正半轴于点E. 将一张正方形纸片沿一对角线对折后,得到一个等腰三角形,再沿底边上的高线对折,把得到的图形(如图)沿虚线剪开,打开阴影部分并铺开,此图形的对称轴有( )
将一张正方形纸片沿一对角线对折后,得到一个等腰三角形,再沿底边上的高线对折,把得到的图形(如图)沿虚线剪开,打开阴影部分并铺开,此图形的对称轴有( )