题目内容
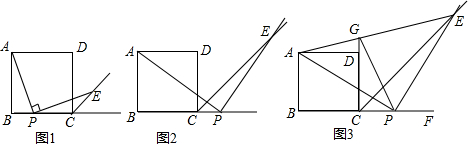
17.在正方形ABCD中,点P是射线BC上任意一点(不与点B、C重合),连接AP,过点P作AP的垂线交正方形的外角∠DCF的平分线于点E.(1)如图1,当点P在BC边上时,判断线段AP、PE的大小关系,并说明理由;
(2)如图2,当点P在BC的延长线上时,(1)中结论是否成立,若成立,请证明;若不成立,请说明理由;
(3)如图3,在(2)的条件下,连接AE交CD的延长线于点G,连接GP,请写出三条线段GP、BP、GD的数量关系并证明.
分析 (1)先判断出∠AHP=∠PCE,再利用互余判断出∠BAP=∠CPE,进而判断出△AHP≌△PCE(ASA),即可得出结论;
(2)同(1)的方法即可得出结论;
(3)先构造全等三角形,判断出AQ=AQ,∠BAQ=∠DAG,进而判断出△PAQ≌△PAG即可得出PG=PQ,最后用等量代换即可得出结论.
解答 解:(1)如图1,
在正方形的边AB上取一点H,使BH=BP,
∵四边形ABCD是正方形,
∴∠ABC=∠DCF=90°,AB=CB,
∴AH=PC,∠BHP=45°,
∴∠AHP=135°,
∵CE是∠DCF的平分线,
∴∠ECF=45°,
∴∠PCE=135°,
∴∠AHP=∠PCE,
∵AP⊥PE,
∴∠APB+∠EPC=90°,
∵∠APB+∠BAP=90°,
∴∠BAP=∠CPE,
在△AHP和△PCE中,$\left\{\begin{array}{l}{∠PAH=∠EPC}\\{AH=PC}\\{∠AHP=∠PCE}\end{array}\right.$,
∴△AHP≌△PCE(ASA),
∴AP=PE;
(2)AP=PE,
理由:如图2,
∵四边形ABCD是正方形,
∴∠B=∠DCF=90°,AB=AC,
在BA的延长线上取一点H,使BH=BP,
∴AH=CP,
在△HBP中,BH=BP,
∴∠BHP=45°,
∵CE是∠DCF的平分线,
∴∠PCE=45°,
∴∠AHP=∠PCE=45°,
∵AP⊥PE,
∴∠EPF+∠APB=90°,
∵∠APB+∠BAP=90°,
∴∠BAP=∠EPF,
∵∠BAP+∠HAP=180°,∠EPF+∠CPE=180°,
∴∠HAP=∠CPE,
在△HAP和△CPE中,$\left\{\begin{array}{l}{∠AHP=∠PCE}\\{AH=PC}\\{∠HAP=∠CPE}\end{array}\right.$,
∴△HAP≌△CPE(ASA),
∴AP=PE,
(3)PG+DG=PB,
理由:如图3, 在BC上取一点Q,使BQ=DG,
在BC上取一点Q,使BQ=DG,
∵四边形ABCD是正方形,
∴∠BAD=∠B=∠ADG=90°,AB=AD,
∴△ABQ≌△ADG(SAS),
∴AQ=AQ,∠BAQ=∠DAG,
∴∠GAQ=90°,
由(2)知,AP=EP,
∵∠APE=90°,
∴∠PAE=45°,
∴∠PAQ=45°=∠PAG,
在△PAQ和△PAG中,$\left\{\begin{array}{l}{AQ=AG}\\{∠PAQ=∠PAG=45°}\\{AP=AP}\end{array}\right.$,
∴△PAQ≌△PAG,
∴PQ=PG,
∵PQ=PB-BQ=PB-DG,
∴PG=PB-DG,
即:PG+DG=PB.
点评 此题是四边形综合题,主要考查了正方形的性质,垂直的意义,全等三角形的判定和性质,角平分线的意义,解本题的关键是构造全等三角形,是一道中考常考题.

 如图,直线y1=$\frac{3}{2}$x与直线y2=-$\frac{1}{2}$x+2交于点A,若y1≤y2,则( )
如图,直线y1=$\frac{3}{2}$x与直线y2=-$\frac{1}{2}$x+2交于点A,若y1≤y2,则( )| A. | x≥1 | B. | x≤1 | C. | x$≥\frac{3}{2}$ | D. | x$≤\frac{3}{2}$ |
| A. | 调查涪陵电视台节目《晚间播报》的收视率 | |
| B. | 调查涪陵市民对皮影表演艺术的喜爱程度 | |
| C. | 调查涪陵城区居民对“武陵山大裂谷”的知晓率 | |
| D. | 调查我国首艘宇宙飞船“天舟一号”的零部件质量 |
 在△ABC中∠A=63°,MN∥BC,若∠AEN=133°,则∠B的度数为70°.
在△ABC中∠A=63°,MN∥BC,若∠AEN=133°,则∠B的度数为70°.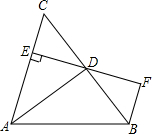 如图,AD是△ABC的角平分线,DE⊥AC,垂足为E,BF∥AC交ED的延长线于点F,若BC恰好平分∠ABF,AE=2BF.给出下列四个结论:①DE=DF;②DB=DC;③AD⊥BC;④AB=2BF,其中正确的结论有①②③.
如图,AD是△ABC的角平分线,DE⊥AC,垂足为E,BF∥AC交ED的延长线于点F,若BC恰好平分∠ABF,AE=2BF.给出下列四个结论:①DE=DF;②DB=DC;③AD⊥BC;④AB=2BF,其中正确的结论有①②③.