题目内容
14.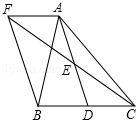 如图,点D是△ABC的边BC上一点,点E是AD的中点,过点A作AF∥BC,交CE的延长线于F,连接BF.
如图,点D是△ABC的边BC上一点,点E是AD的中点,过点A作AF∥BC,交CE的延长线于F,连接BF.(1)试说明△AEF≌△DEC;
(2)若点D是BC的中点,则BF与AD有怎样的数量关系和位置变化?说明理由.
分析 (1)根据两直线平行,内错角相等求出∠AFE=∠DCE,然后利用“角角边”证明△AEF和△DEC全等;
(2)由△AEF≌△DEC得到:AF=DC且AF∥DC,BD=DC,可得四边形AFDC是平行四边形,则BF∥AD且BF=AD.
解答  证明:(1)∵AF∥BC,
证明:(1)∵AF∥BC,
∴∠AFE=∠DCE,
∵点E为AD的中点,
∴AE=DE,
在△AEF和△DEC中,
$\left\{\begin{array}{l}{∠AFE=∠DCE}\\{∠AEF=∠DEC}\\{AE=DE}\end{array}\right.$,
∴△AEF≌△DEC(AAS);
(2)由(1)知,△AEF≌△DEC,
∴AF=CD,
又∵BD=CD,
∴AF=BD,
又∵AF∥BD,
∴四边形AFBD是平行四边形,
∴BF∥AD且BF=AD.
点评 本题考查平行四边形的判定和全等三角形的判定与性质.要熟知这些判定定理才会灵活运用,根据性质才能得到需要的相等关系.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
5. 如图,直线y1=$\frac{3}{2}$x与直线y2=-$\frac{1}{2}$x+2交于点A,若y1≤y2,则( )
如图,直线y1=$\frac{3}{2}$x与直线y2=-$\frac{1}{2}$x+2交于点A,若y1≤y2,则( )
 如图,直线y1=$\frac{3}{2}$x与直线y2=-$\frac{1}{2}$x+2交于点A,若y1≤y2,则( )
如图,直线y1=$\frac{3}{2}$x与直线y2=-$\frac{1}{2}$x+2交于点A,若y1≤y2,则( )| A. | x≥1 | B. | x≤1 | C. | x$≥\frac{3}{2}$ | D. | x$≤\frac{3}{2}$ |
9.下列调查中,适宜采用普查方式的是( )
| A. | 调查涪陵电视台节目《晚间播报》的收视率 | |
| B. | 调查涪陵市民对皮影表演艺术的喜爱程度 | |
| C. | 调查涪陵城区居民对“武陵山大裂谷”的知晓率 | |
| D. | 调查我国首艘宇宙飞船“天舟一号”的零部件质量 |
 如图,在△ABC中,∠C=90°,CD⊥AB于D,AC=6,BC=8.求CD的长.
如图,在△ABC中,∠C=90°,CD⊥AB于D,AC=6,BC=8.求CD的长.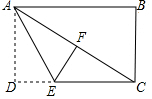 如图,在矩形ABCD中,将△ADE沿AE折叠,点D刚好落在对角线AC上的F点.
如图,在矩形ABCD中,将△ADE沿AE折叠,点D刚好落在对角线AC上的F点.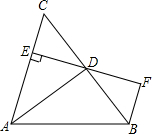 如图,AD是△ABC的角平分线,DE⊥AC,垂足为E,BF∥AC交ED的延长线于点F,若BC恰好平分∠ABF,AE=2BF.给出下列四个结论:①DE=DF;②DB=DC;③AD⊥BC;④AB=2BF,其中正确的结论有①②③.
如图,AD是△ABC的角平分线,DE⊥AC,垂足为E,BF∥AC交ED的延长线于点F,若BC恰好平分∠ABF,AE=2BF.给出下列四个结论:①DE=DF;②DB=DC;③AD⊥BC;④AB=2BF,其中正确的结论有①②③.