题目内容
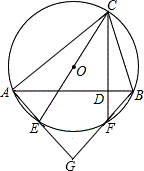 已知△ABC内接于⊙O,CE是⊙O的直径,CD⊥AB于D,CD延长线交⊙O于F,AE,BF的延长线相交于点G.求证:
已知△ABC内接于⊙O,CE是⊙O的直径,CD⊥AB于D,CD延长线交⊙O于F,AE,BF的延长线相交于点G.求证:(1)∠ACD=∠BCE;
(2)GA=GB.
考点:圆周角定理,圆心角、弧、弦的关系
专题:证明题
分析:(1)首先连接BE,由CE是⊙O的直径,可得∠CBE=90°,又由CD⊥AB,可证得∠ACD=∠BCE;
(2)由圆周角定理可得∠BAE=∠BCE,∠ACD=∠ABF,又由∠ACD=∠BCE,即可证得结论.
(2)由圆周角定理可得∠BAE=∠BCE,∠ACD=∠ABF,又由∠ACD=∠BCE,即可证得结论.
解答: 证明:(1)连接BE,
证明:(1)连接BE,
∵CE是⊙O的直径,
∴∠CBE=90°,
∴∠CEB+∠BCE=90°,
∵CD⊥AB,
∴∠ACD+∠BAC=90°,
∵∠CEB=∠BAC,
∴∠ACD=∠BCE;
(2)∵∠ACD=∠BCE,∠BAE=∠BCE,∠ACD=∠ABF,
∴∠BAE=∠ABF,
∴GA=GB.
 证明:(1)连接BE,
证明:(1)连接BE,∵CE是⊙O的直径,
∴∠CBE=90°,
∴∠CEB+∠BCE=90°,
∵CD⊥AB,
∴∠ACD+∠BAC=90°,
∵∠CEB=∠BAC,
∴∠ACD=∠BCE;
(2)∵∠ACD=∠BCE,∠BAE=∠BCE,∠ACD=∠ABF,
∴∠BAE=∠ABF,
∴GA=GB.
点评:此题考查了圆周角定理以及等腰三角形的判定.此题难度适中,注意掌握辅助线的作法,注意掌握数形结合思想的应用.

练习册系列答案
相关题目
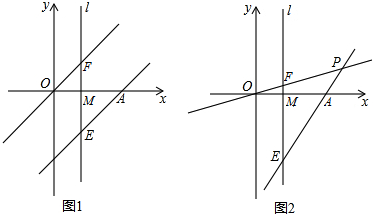
 如图,小明同学在南北方向的滨河路A处,测得体育馆P在北偏西30°方向上,向北前行500米到达B处,测得体育馆P在北偏西75°方向上,求体育馆P到滨河路的距离PC.(结果精确到0.1米,
如图,小明同学在南北方向的滨河路A处,测得体育馆P在北偏西30°方向上,向北前行500米到达B处,测得体育馆P在北偏西75°方向上,求体育馆P到滨河路的距离PC.(结果精确到0.1米,| 3 |
下列调查中,样本具有代表性的是( )
| A、在运动场调查当代青年业余时间娱乐的主要方式 |
| B、在音乐厅了解市民对古典名著的了解程度 |
| C、调查班级学号为单数的同学,以了解同学们身高情况 |
| D、在眼科医院调查4~6岁学龄前儿童患沙眼的比例 |
如图所示是△ABC位似图形的几种画法,其中正确的是个数是( )


| A、1 | B、2 | C、3 | D、4 |
 如图,AB、CD交于点O,∠AOE=90°,若∠AOC:∠COE=5:4,求∠AOD的度数.
如图,AB、CD交于点O,∠AOE=90°,若∠AOC:∠COE=5:4,求∠AOD的度数.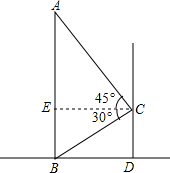 如图所示,某中学的教学楼前有一棵大树AB,小明在教学楼的C处测得树顶A的仰角为45°,底部B的俯角为30°,已知大树与教学楼之间的水平距离BD=6m,求AB(结果保留根号).
如图所示,某中学的教学楼前有一棵大树AB,小明在教学楼的C处测得树顶A的仰角为45°,底部B的俯角为30°,已知大树与教学楼之间的水平距离BD=6m,求AB(结果保留根号). 直线AB,CD被直线EF所截,交AB,CD于点M,N,NH是一条射线,图中共有多少对同位角?多少对内错角?多少对同旁内角?分别指出这些角?
直线AB,CD被直线EF所截,交AB,CD于点M,N,NH是一条射线,图中共有多少对同位角?多少对内错角?多少对同旁内角?分别指出这些角? 如图,△ABF≌△CDE,∠B=30°,∠DCF=20°,求∠EFC的度数.
如图,△ABF≌△CDE,∠B=30°,∠DCF=20°,求∠EFC的度数.