下列方程(组)中.①x+2=0 ②3x-2y=1 ③xy+1=0 ④2x-$\frac{1}{x}$=1 ⑤$\left\{\begin{array}{l}{x+y=1}\\{x-y=3}\end{array}\right.$ ⑥$\left\{\begin{array}{l}{2x-y=0}\\{x+z=1}\end{array}\right.$是一元一次方程的是①.是二元一次方程的是� 题目和参考答案——青夏教育精英家教网——

题目内容

3．下列方程（组）中，①x+2=0 ②3x-2y=1 ③xy+1=0 ④2x-$\frac{1}{x}$=1 ⑤$\left\{\begin{array}{l}{x+y=1}\\{x-y=3}\end{array}\right.$ ⑥$\left\{\begin{array}{l}{2x-y=0}\\{x+z=1}\end{array}\right.$是一元一次方程的是①，是二元一次方程的是②，是二元一次方程组的是⑤．

分析根据一元一次方程是整式方程中只含有一个未知数且未知数的最高次数是一次的方程，整式方程中含有两个未知数且未知数的次数是1次的方程，组成二元一次方程组的两个方程应共含有两个未知数，且未知数的项最高次数都应是一次的整式方程．

解答解：①x+2=0 ②3x-2y=1 ③xy+1=0 ④2x-$\frac{1}{x}$=1 ⑤$\left\{\begin{array}{l}{x+y=1}\\{x-y=3}\end{array}\right.$ ⑥$\left\{\begin{array}{l}{2x-y=0}\\{x+z=1}\end{array}\right.$是一元一次方程的是①，是二元一次方程的是②，是二元一次方程组的是⑤．
故答案为：①；②；⑤．

点评本题考查了二元一次方程组的定义，熟记一元一次方程，二元一次方程是解题关键，注意二元一次方程组的定义“由两个二元一次方程组成的方程组”．

练习册系列答案

课课练活页卷系列答案

满分试卷期末冲刺100分系列答案

课程标准同步导练系列答案

新经典练与测系列答案

本土教辅名校学案小学生之友系列答案

全优期末真题8套系列答案

期末好卷系列答案

红领巾乐园系列答案

初中英语最佳方案冲刺AB卷系列答案

新中考指南系列答案

相关题目

13．若9x²-（k+1）x+4是完全平方式，则k的值为（　　）

14．甲、乙两个家庭同去一家粮店购买大米两次．两次大米的售价有变化，但两个家庭的购买方式不同，其中甲家庭每次总是买20千克大米，而乙家庭每次用去20元，商店也按价计算卖给乙家庭．设前后两次的米价分别是每千克m元和n元（m＞0，n＞0，m≠n），请问谁的购买方式合算？

11．正比例函数的图象经过点（1，-5），它的解析式是y=-5x．

18．三个连续奇数之和为15，则它们之积为（　　）

8．在△ABC中，如果∠C=55°，∠B-∠C=10°，那么∠A=60°，∠B=65°．

15．计算：
（1）$\sqrt{24}+\sqrt{\frac{2}{3}}-3\sqrt{6}$
（2）$\frac{3}{2+\sqrt{3}}$×$\root{3}{\frac{1}{27}}$-（-2）⁰+|$\sqrt{3}$-$\sqrt{2}$|^-1．

12．根据下列数的规律，它的第100个数是多少？第2015个数又是多少？
-1，$\frac{1}{2}$，-3，$\frac{1}{4}$，-5，$\frac{1}{6}$，-7，$\frac{1}{8}$，…

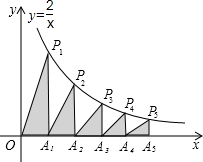如图，在x轴的正半轴上依次截取OA₁=A₁A₂=A₂A₃=A₃A₄=A₄A₅=1，过点A₁、A2、A3、A₄、A₅分别作x轴的垂线与反比例函数y=$\frac{2}{x}$（x≠0）的图象相交于点P₁、P₂、P₃、P₄、P₅，得直角三角形OP₁A₁、A₁P₂A₂、A₂P₃A₃、A₃P₃A₄、A₄P₅A₅并设其面积分别为S₁、S₂、S₃、S₄、S₅，则S₁+S₂+S₃+S₄+S₅的值为$\frac{137}{60}$．