题目内容
如果a=125x+126,c=125x+128,b=125x+127,那么b2+c2-a2-ac-2(a+c)的值为 .
考点:因式分解的应用
专题:
分析:将b2+c2-a2-ac-2(a+c)变形为b2-ac+(c+a)(c-a-2),再将a=125x+126,c=125x+128,b=125x+127代入,根据完全平方公式和平方差公式抵消求解即可.
解答:解:b2+c2-a2-ac-2(a+c)
=b2+(c+a)(c-a)-ac-2(a+c)
=b2-ac+(c+a)(c-a-2)
=(125x+127)2-(125x+127-1)(125x+127+1)+(c+a)(125x+128-125x-126-2)
=(125x+127)2-(125x+127)2+1+0
=1.
故答案为:1.
=b2+(c+a)(c-a)-ac-2(a+c)
=b2-ac+(c+a)(c-a-2)
=(125x+127)2-(125x+127-1)(125x+127+1)+(c+a)(125x+128-125x-126-2)
=(125x+127)2-(125x+127)2+1+0
=1.
故答案为:1.
点评:此题主要考查了因式分解的应用,根据题意正确的利用完全平方公式和平方差公式分解因式是解决问题的关键.同时注意整体思想的运用.

练习册系列答案
相关题目
下列方程组不是三元一次方程组的是( )
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
 已知:B是线段AC上一点.且AB:BC=10:7.又D是线段AC延长线上一点.且BD:AC=11:17.若CD=16.求AB、BC的长.
已知:B是线段AC上一点.且AB:BC=10:7.又D是线段AC延长线上一点.且BD:AC=11:17.若CD=16.求AB、BC的长. 如图,在△ABC中,∠B=50°,AB=22cm,BC=25cm,求△ABC的面积(精确到0.1cm2).
如图,在△ABC中,∠B=50°,AB=22cm,BC=25cm,求△ABC的面积(精确到0.1cm2).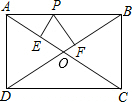 在矩形ABCD中,P为AB上的动点,PE⊥AC于E,PF⊥BD于F,求证:PE+PF为定值.
在矩形ABCD中,P为AB上的动点,PE⊥AC于E,PF⊥BD于F,求证:PE+PF为定值.