题目内容
11.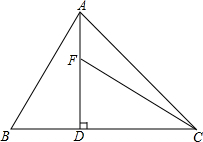 如图,AD⊥BC于D,F在AD上,且CF=AB,若DF=BD,求证:CF⊥AB.
如图,AD⊥BC于D,F在AD上,且CF=AB,若DF=BD,求证:CF⊥AB.
分析 根据SAS证明△ABD与△CFD全等,再利用角的互余证明即可.
解答 证明:在△ABD与△CFD中,
$\left\{\begin{array}{l}{BD=DF}\\{∠ADB=∠CDF=90°}\\{CF=AB}\end{array}\right.$,
∴△ABD≌△CFD(SAS),
∴∠B=∠DFC,
∵∠DFC+∠DCF=90°,
∴∠B+∠DCF=90°,
∴CF⊥AB.
点评 此题考查全等三角形的判定和性质,关键是根据SAS证明△ABD与△CFD全等,再利用角的互余证明.

练习册系列答案
相关题目
 如图,在△ABC中,∠ABC=90°,D为AB延长线上一点,点E在BC边上且BE=BD,连结AE、DE、DC,AE=DC.
如图,在△ABC中,∠ABC=90°,D为AB延长线上一点,点E在BC边上且BE=BD,连结AE、DE、DC,AE=DC.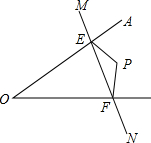 如图,点P在∠AOB内部,点M,N分别是点P关于直线AO、BO的对称点,若△PEF的周长为15,求MN的长.
如图,点P在∠AOB内部,点M,N分别是点P关于直线AO、BO的对称点,若△PEF的周长为15,求MN的长.
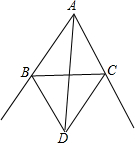 如图,已知,△ABC的∠B,∠C的外角平分线交于点D,AD是∠BAC的平分线吗?说明理由.
如图,已知,△ABC的∠B,∠C的外角平分线交于点D,AD是∠BAC的平分线吗?说明理由.