题目内容
19. 如图,抛物线y=-$\frac{1}{2}$x2+bx+c与y轴交于点C,与x轴交于A、B两点(点A在原点左侧,点B在原点右侧),且∠ACB=90°,tan∠BAC=$\frac{1}{2}$.
如图,抛物线y=-$\frac{1}{2}$x2+bx+c与y轴交于点C,与x轴交于A、B两点(点A在原点左侧,点B在原点右侧),且∠ACB=90°,tan∠BAC=$\frac{1}{2}$.①求抛物线的解析式;
②若抛物线顶点为P,求四边形APCB的面积.
分析 ①由y=-$\frac{1}{2}$x2+bx+c=c,可求得C(0,c),由tan∠BAC=$\frac{1}{2}$,可设A(-2c,0),B($\frac{1}{2}$c,0),把A(-2c,0),B($\frac{1}{2}$c,0)代入y=-$\frac{1}{2}$x2+bx+c=c求得b,c,即可求得求抛物线的解析式;
②解方程-$\frac{1}{2}$x2-$\frac{3}{10}$x+$\frac{1}{5}$=0可求得A,B点的坐标,由于四边形APCB的面积=S△AOP+S△POC+S△COB,根据三角形的面积公式即可求得结论.
解答 解:①令x=0则y=-$\frac{1}{2}$x2+bx+c=c,
∴C(0,c),
∵tan∠BAC=$\frac{1}{2}$,
∴A(-2c,0),
∠ACB=90°,
∴∠BCO=∠BAC,
∴OB=$\frac{1}{2}$OC=$\frac{1}{2}$c,
∴B($\frac{1}{2}$c,0),
把A(-2c,0),B($\frac{1}{2}$c,0)代入y=-$\frac{1}{2}$x2+bx+c=c得,$\left\{\begin{array}{l}{-\frac{1}{2}(-2c)^{2}+b(-2c)+c=0}\\{-\frac{1}{2}(\frac{1}{2}c)^{2}+b•\frac{1}{2}c+c=0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{b=-\frac{3}{10}}\\{c=\frac{1}{5}}\end{array}\right.$,
求抛物线的解析式为y=-$\frac{1}{2}$x2-$\frac{3}{10}$x+$\frac{1}{5}$;
②y=-$\frac{1}{2}$x2-$\frac{3}{10}$x+$\frac{1}{5}$=-$\frac{1}{2}$(x+$\frac{3}{10}$)2+$\frac{49}{100}$,
∴P(-$\frac{3}{10}$,$\frac{49}{100}$),
令-$\frac{1}{2}$x2-$\frac{3}{10}$x+$\frac{1}{5}$=0,解得:x1=-1,x2=$\frac{2}{5}$,
∴A(-1,0),B($\frac{2}{5}$,0)
连接AP,PC,CB,PO,则四边形APCB的面积=S△AOP+S△POC+S△COB=$\frac{1}{2}$×1×$\frac{49}{100}$+$\frac{1}{2}$×$\frac{1}{5}$×$\frac{3}{10}$+$\frac{1}{2}$×$\frac{2}{5}$×$\frac{1}{5}$=$\frac{9}{100}$.
点评 本题主要考查了待定系数法确定函数关系式,三角函数的定义,求二次函数的顶点坐标与x轴的交点坐标,割补法求四边形的面积,能够把四边形APCB分割成三个三角形△AOP.△POC,△COB是解题的关键.

(1)求购买A型和B型公交车每辆各需多少万元?
(2)预计在该线路上A型和B型公交车每辆年均载客量分别为60万人次和100万人次.若该公司购买A型公交车x辆,完成下表:
| 数量(辆) | 购买总费用(万元) | 载客总量(万人次) | |
| A型车 | x | 100x | 60x |
| B型车 | 10-x | 150(10-x) | 100(10-x) |
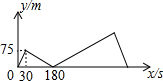 甲、乙两人在直线道路上同起点,同终点,同方向,分别以不同的速度匀速跑步1500m,先到终点的人原地休息,已知甲先出发30s后,乙才出发,甲、乙两人的距离y(m)与甲出发的时间x(s)之间的关系如图所示,下列说法中错误的是( )
甲、乙两人在直线道路上同起点,同终点,同方向,分别以不同的速度匀速跑步1500m,先到终点的人原地休息,已知甲先出发30s后,乙才出发,甲、乙两人的距离y(m)与甲出发的时间x(s)之间的关系如图所示,下列说法中错误的是( )| A. | 甲的速度是2.5m/s,乙的速度为3m/s | |
| B. | 乙出发150秒后追上了甲 | |
| C. | 乙到达终点时,甲距终点250m | |
| D. | 甲到达终点比乙晚了70s |
| A. | m≤2 | B. | m<-2 | C. | m>2 | D. | 0<m≤2 |
 已知圆形纸片⊙O的直径为2,将其沿着两条互相垂直的直径折叠,得到四层的扇形,将最上的一层“撑”开来,“鼓”成一个无底的圆锥,则这个圆锥的高是( )
已知圆形纸片⊙O的直径为2,将其沿着两条互相垂直的直径折叠,得到四层的扇形,将最上的一层“撑”开来,“鼓”成一个无底的圆锥,则这个圆锥的高是( )| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | 1 |
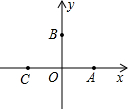 如图,在平面直角坐标系中,点A,B,C的坐标分别为(1,0),(0,1)(-1,0).一个电动玩具从坐标原点O出发,第一次跳跃到点P1.使得点P1与点O关于点A成中心对称;第二次跳跃到点P2,使得点P2与点P1关于点B成中心对称;第三次跳跃到点P3,使得点P3与点P2关于点C成中心对称;第四次跳跃到点P4,使得点P4与点P3关于点A成中心对称;第五次跳跃到点P5,使得点P5与点P4关于点B成中心对称;…照此规律重复下去,则点P2017的坐标为(2,0).
如图,在平面直角坐标系中,点A,B,C的坐标分别为(1,0),(0,1)(-1,0).一个电动玩具从坐标原点O出发,第一次跳跃到点P1.使得点P1与点O关于点A成中心对称;第二次跳跃到点P2,使得点P2与点P1关于点B成中心对称;第三次跳跃到点P3,使得点P3与点P2关于点C成中心对称;第四次跳跃到点P4,使得点P4与点P3关于点A成中心对称;第五次跳跃到点P5,使得点P5与点P4关于点B成中心对称;…照此规律重复下去,则点P2017的坐标为(2,0).