题目内容
9. 已知圆形纸片⊙O的直径为2,将其沿着两条互相垂直的直径折叠,得到四层的扇形,将最上的一层“撑”开来,“鼓”成一个无底的圆锥,则这个圆锥的高是( )
已知圆形纸片⊙O的直径为2,将其沿着两条互相垂直的直径折叠,得到四层的扇形,将最上的一层“撑”开来,“鼓”成一个无底的圆锥,则这个圆锥的高是( )| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | 1 |
分析 先求得圆锥的底面半径,然后利用底面半径、高及母线构成直角三角形求解即可.
解答 解:由题意知该无敌圆锥是由半圆O围成的,其半径为1,折叠后扇形的弧长为π,
设圆锥的底面半径为r,
则2πr=π,
解得:r=$\frac{1}{2}$,
∴圆锥的高为$\sqrt{{1}^{2}-(\frac{1}{2})^{2}}$=$\frac{\sqrt{3}}{2}$,
故选C.
点评 此题主要考查了圆锥的计算,解答此题的关键是求出扇形围成的圆锥的底面半径是多少.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
4. 如图,在矩形ABCD中,AB=4,AD=2,点E、F都对角线AC上,且AE=EF=FC,则线段BE和DF的距离为( )
如图,在矩形ABCD中,AB=4,AD=2,点E、F都对角线AC上,且AE=EF=FC,则线段BE和DF的距离为( )
 如图,在矩形ABCD中,AB=4,AD=2,点E、F都对角线AC上,且AE=EF=FC,则线段BE和DF的距离为( )
如图,在矩形ABCD中,AB=4,AD=2,点E、F都对角线AC上,且AE=EF=FC,则线段BE和DF的距离为( )| A. | $\frac{2\sqrt{5}}{3}$ | B. | 1 | C. | $\frac{3\sqrt{17}}{17}$ | D. | $\frac{4\sqrt{17}}{17}$ |
13.下列方程中,属于二元一次方程的是( )
| A. | 4x+2(8-5x)=3 | B. | $\frac{1}{5}$x-3y=6 | C. | x2+4y=9 | D. | xy+2x=5 |
 如图,抛物线y=-$\frac{1}{2}$x2+bx+c与y轴交于点C,与x轴交于A、B两点(点A在原点左侧,点B在原点右侧),且∠ACB=90°,tan∠BAC=$\frac{1}{2}$.
如图,抛物线y=-$\frac{1}{2}$x2+bx+c与y轴交于点C,与x轴交于A、B两点(点A在原点左侧,点B在原点右侧),且∠ACB=90°,tan∠BAC=$\frac{1}{2}$.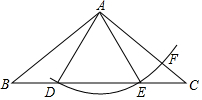 如图,在△ABC中,AB=AC,D在边BC上,以A为圆心,AD长为半径画圆弧,交边BC的另一点E,交边AC于F,连接AE,EF.
如图,在△ABC中,AB=AC,D在边BC上,以A为圆心,AD长为半径画圆弧,交边BC的另一点E,交边AC于F,连接AE,EF. 如图,在平面直角坐标系xOy中,抛物线y=x2-(1-m)x+3m经过点A(-1,0),且与y轴相交于点B.
如图,在平面直角坐标系xOy中,抛物线y=x2-(1-m)x+3m经过点A(-1,0),且与y轴相交于点B.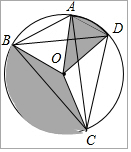 已知四边形ABCD是⊙O的内接垂直四边形,AB=3,CD=4,连接OA,OB,OC,OD,求图中扇形AOD和扇形BOC面积的和(图中阴影部分).
已知四边形ABCD是⊙O的内接垂直四边形,AB=3,CD=4,连接OA,OB,OC,OD,求图中扇形AOD和扇形BOC面积的和(图中阴影部分).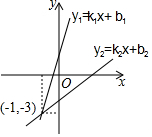 如图,平面直角坐标系xOy中,直线y1=k1x+b1的图象与直线y2=k2x+b2的图象相交于点(-1,-3),当y1<y2时,实数x的取值范围为x<-1.
如图,平面直角坐标系xOy中,直线y1=k1x+b1的图象与直线y2=k2x+b2的图象相交于点(-1,-3),当y1<y2时,实数x的取值范围为x<-1.