Question

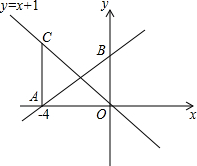如图，在平面直角坐标系xOy中，直线l与x轴交于点A（-4，0），与y轴的正半轴交于点B．点C在直线y=-x+1上，且CA⊥x轴于点A．
（1）求点C的坐标；
（2）若点D是OA的中点，点E是y轴上一个动点，当EC+ED最小时，求此时点E的坐标；
（3）若点A恰好在BC的垂直平分线上，点F在x轴上，且△ABF是以AB为腰的等腰三角形，请直接写出所有满足条件的点F的坐标．

Answer 1

考点：一次函数综合题

专题：

分析：（1）根据自变量的值，可得相应的函数值；
（2）根据根据线段垂直平分线的性质，可得D点关于y轴的对称点，根据两点之间线段最短，可得CG，根据待定系数法，可得函数解析式，可得点E的坐标，
（3）根据垂直平分线的性质，可得AC与AB的关系，根据等腰三角形的定义，可得答案．

解答：解：（1）由点C在直线y=-x+1上，当x=-4时，y=-（-4）+1=5，即C（-4，5）；
（2）有D是OA的中点，得D（-2，0），D点关于y轴的对称点是G（2，0），
连接CG，交y轴于E点，EC+ED=CE，设CE的解析式为y=kx+b，
把C、G点的坐标代入y=kx+b，得

2k+b=0 -4k+b=5

．解得

k=- 5 6 b= 5 3

，
即E点坐标（0，

5

3

）；
（3）由点A恰好在BC的垂直平分线上，得AC=AB=5，
点F在x轴上，且△ABF是以AB为腰的等腰三角形，得
AF=5．
当点F在A点的左边时，-4-5=-9，即F点坐标（-9，0），
当点F在A点的右边时，-4+5=-1，即F点坐标（-1，0）．

点评：本题考查了一次函数综合题，（1）利用了自变量与函数值的相应关系，（2）利用了轴对称的性质，线段的性质；（3）利用了线段垂直平分线的性质，等腰三角形的定义，要分类讨论：当点F在A点的左边时，当点F在A点的右边时，以防漏掉．