题目内容
在Rt△ABC中,已知∠ACB=90°,BC=1,AB=2,那么下列结论正确的是( )
A、sinA=
| ||||
B、tanA=
| ||||
C、cosB=
| ||||
D、cotB=
|
考点:特殊角的三角函数值
专题:
分析:直接利用锐角三角函数关系分别求出即可.
解答: 解:如图所示:
解:如图所示:
∵∠ACB=90°,BC=1,AB=2,
∴AC=
,
∴sinA=
,故选项A错误;
tanA=
=
,故选项B错误;
cosB=
,故选项C错误;
cotB=
,正确.
故选:D.
 解:如图所示:
解:如图所示:∵∠ACB=90°,BC=1,AB=2,
∴AC=
| 3 |
∴sinA=
| 1 |
| 2 |
tanA=
| 1 | ||
|
| ||
| 2 |
cosB=
| 1 |
| 2 |
cotB=
| ||
| 3 |
故选:D.
点评:此题主要考查了锐角三角函数关系,正确记忆相关比例关系是解题关键.

练习册系列答案
相关题目
 如图是由五个相同的小立方块搭成的几何体,这个几何体的左视图是( )
如图是由五个相同的小立方块搭成的几何体,这个几何体的左视图是( )A、 |
B、 |
C、 |
D、 |
分式方程
+
=
的解为( )
| 2 |
| x+1 |
| 3 |
| x-1 |
| 6 |
| x2-1 |
| A、1 | B、-1 | C、2 | D、无解 |
已知⊙M与⊙N的半径分别为1和5,若两圆相切,那么这两圆的圆心距MN的长等于( )
| A、4 | B、6 | C、4或5 | D、4或6 |
已知两圆半径分别是3和4,若两圆内切,则两圆的圆心距为( )
| A、1或7 | B、1 | C、7 | D、2 |
下列四个交通标志中,轴对称图形是( )
A、 |
B、 |
C、 |
D、 |
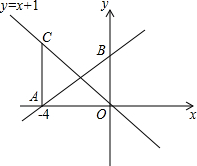 如图,在平面直角坐标系xOy中,直线l与x轴交于点A(-4,0),与y轴的正半轴交于点B.点C在直线y=-x+1上,且CA⊥x轴于点A.
如图,在平面直角坐标系xOy中,直线l与x轴交于点A(-4,0),与y轴的正半轴交于点B.点C在直线y=-x+1上,且CA⊥x轴于点A.