题目内容
 如图,平行于y轴的直尺(一部分)与反比例函数y=
如图,平行于y轴的直尺(一部分)与反比例函数y=| k |
| x |
(1)求这个反比例函数的解析式;
(2)求梯形ABCD的面积.
考点:反比例函数的应用
专题:
分析:(1)将已知点的坐标代入即可利用待定系数法确定反比例函数的解析式;
(2)根据点C的横坐标为4且点C在反比例函数的图象上得到点C的坐标,从而求得梯形ABDC的面积.
(2)根据点C的横坐标为4且点C在反比例函数的图象上得到点C的坐标,从而求得梯形ABDC的面积.
解答:解:(1)由题意可知A(2,3),设反比例函数的解析式为y=
,
∵反比例函数过A(2,3),
∴k=2×3=6,
∴反比例函数的解析式为y=
;
(2)∵C的横坐标为4,且点C在y=
上,
∴点C的坐标表为(4,
),
∴S梯形ABDC=
(AB+CD)×BD=
(3+1.5)×2=4.5
| k |
| x |
∵反比例函数过A(2,3),
∴k=2×3=6,
∴反比例函数的解析式为y=
| 6 |
| x |
(2)∵C的横坐标为4,且点C在y=
| 6 |
| x |
∴点C的坐标表为(4,
| 3 |
| 2 |
∴S梯形ABDC=
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题考查了反比例函数的应用,解题的关键是从实际问题中抽象出反比例函数模型,难度不大.

练习册系列答案
相关题目
2012年全国参加普通高等学校招生考试的人数约为9150000人,其中9150000用科学记数法表示为( )
| A、9.15×104 |
| B、9.15×105 |
| C、9.15×106 |
| D、9.15×107 |
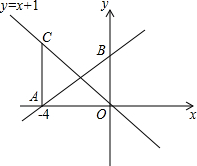 如图,在平面直角坐标系xOy中,直线l与x轴交于点A(-4,0),与y轴的正半轴交于点B.点C在直线y=-x+1上,且CA⊥x轴于点A.
如图,在平面直角坐标系xOy中,直线l与x轴交于点A(-4,0),与y轴的正半轴交于点B.点C在直线y=-x+1上,且CA⊥x轴于点A.